已知平面
上的动点
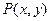及两定点A（-2，0），B（2，0），直线PA，PB的斜率分别是
，
，且·
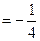。（1）求动点P的轨迹C的方程；
（2）已知直线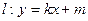
与曲线C交于M，N两点，且直线BM，BN的斜率都存在并满足
·
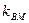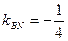，求证：直线
过原点。
设数列
。
(I) 把算法流程图补充完整：
①处的语句应为；
②处的语句应为；
(Ⅱ) 虚框内的逻辑结构为；
(Ⅲ) 根据流程图写出程序：
分别写出下列命题的逆命题，否命题，逆否命题，并判断其真假．
（1）矩形的对角线相等且互相平分；
（2）正偶数不是质数．
已知函数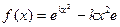
(
)（
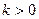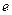为自然对数的底数）
（1）求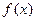
的极值
（2）对于数列
,
(
)
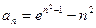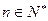①证明:
②考察关于正整数
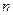的方程
是否有解，并说明理由
已知抛物线
的准线为
，焦点为
，圆
的圆心在
轴的正半轴上，且与
轴相切，过原点
作倾斜角为
的直线
，交
于点
，交圆于另一点
，且
（1）求圆和抛物线C的方程；
（2）若
为抛物线C上的动点，求
的最小值；
（3）过上的动点Q向圆作切线，切点为S，T，
求证：直线ST
恒过一个定点，并求该定点的坐标.
如图，正四棱柱
中，
，点
在
上且
(1)证明：
平面
；
(2)求二面角
的余弦值．