如图,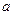 ,
,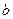 是异面直线,
是异面直线,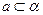 ,
, ,
,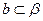 ,
,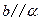 .求证
.求证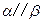 .
.
 |
|||
 |
某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格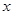 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式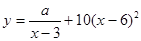 ,其中
,其中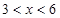 ,
,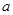 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
(1) 求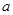 的值;
的值;
(2) 若该商品的成本为3元/千克, 试确定销售价格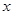 的值,使商场每日销售该商品所
的值,使商场每日销售该商品所
获得的利润最大.(利润=销售额-成本)
已知点A 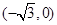 和B
和B 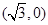 ,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与经过点(2,0)且倾斜角为
,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与经过点(2,0)且倾斜角为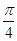 的直线交于D、E两点
的直线交于D、E两点
(1)求点C的轨迹方程;
(2)求线段DE的长
设椭圆C:  过点(0,4),(5,0).
过点(0,4),(5,0).
(1)求C的方程;
(2)求过点(3,0)且斜率为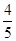 的直线被椭圆C所截线段的中点坐标
的直线被椭圆C所截线段的中点坐标
甲、乙两射击运动员分别对一目标射击 次,甲射中的概率为
次,甲射中的概率为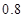 ,乙射中的概率为
,乙射中的概率为 ,求:
,求:
(1)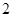 人都射中目标的概率;
人都射中目标的概率;
(2)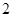 人中恰有
人中恰有 人射中目标的概率;
人射中目标的概率;
(3)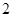 人至少有
人至少有 人射中目标的概率
人射中目标的概率
设函数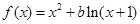 ,其中
,其中 .
.
(Ⅰ)当 时,判断函数
时,判断函数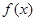 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)求函数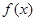 的极值点;
的极值点;
(Ⅲ)证明对任意的正整数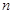 ,不等式
,不等式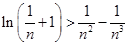 都成立.
都成立.