当 为何值时,直线
为何值时,直线 .
.
(1) 倾斜角为 ; (2)在
; (2)在 轴上的截距为1.
轴上的截距为1.
用0,1,2,3,4,5六个数字:
(1)能组成多少个没有重复数字的四位数;
(2)能组成多少个没有重复数字的四位偶数;
(3)能组成多少个能被5整除的没有重复数字的四位数;
(4)能组成多少个没有重复数字的比3210大的四位数。
已知复数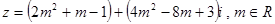 ,当实数m取什么值时,复数z:
,当实数m取什么值时,复数z:
(1)是实数;
(2)是纯虚数;
(3)共轭复数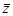 对应的点在第一象限。
对应的点在第一象限。
已知复数 ,计算:
,计算:
(1) 的值;
的值;
(2) 的值。
的值。
(本小题满分12分)
已知数列 的前三项与数列
的前三项与数列 的前三项对应相同,且
的前三项对应相同,且 对任意的
对任意的 都成立,数列
都成立,数列 是等差数列
是等差数列
(1)求数列 与
与 的通项公式;
的通项公式;
(2)是否存在 使得
使得 ?请说明理由。
?请说明理由。
(本小题满分12分)
如图,三棱柱ABC—A1B1C1中,底面为正三角形,侧棱与底面垂直,D是BC的中点,AA1=AB=1。
(1)求证:A1C∥平面AB1D;
(2)求点C到平面AB1D的距离。