|
已知双曲线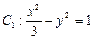 的左、右焦点分别是F1、F2.
的左、右焦点分别是F1、F2.
 的点P的坐标;
的点P的坐标;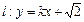 与椭圆恒有两个不同的交点A和B,且
与椭圆恒有两个不同的交点A和B,且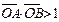 (其中O为坐标原点),求k的取值范围.
(其中O为坐标原点),求k的取值范围.(本小题满分14分)已知函数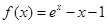 ,
,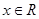 , 其中,
, 其中,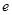 是自然对数的底数.函数
是自然对数的底数.函数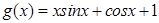 ,
,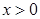 .
.
(Ⅰ)求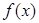 的最小值;
的最小值;
(Ⅱ)将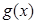 的全部零点按照从小到大的顺序排成数列
的全部零点按照从小到大的顺序排成数列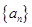 ,求证:
,求证:
(1)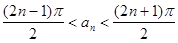 ,其中
,其中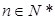 ;
;
(2)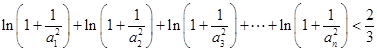 .
.
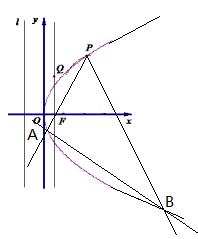
(本小题满分13分)如图,设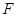 为抛物线
为抛物线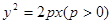 的焦点,
的焦点,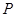 是抛物线上一定点,其
是抛物线上一定点,其
坐为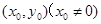 ,
,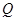 为线段
为线段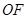 的垂直平分线上一点,且点
的垂直平分线上一点,且点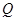 到抛物线的准线
到抛物线的准线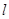 的距离为
的距离为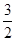 .
.
(Ⅰ)求抛物线的方程;
(Ⅱ)过点P任作两条斜率均存在的直线PA、PB,分别与抛物线交于点A、B,如图示,若直线AB的斜率为定值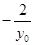 ,求证:直线PA、PB的倾斜角互补.
,求证:直线PA、PB的倾斜角互补.
(本小题满分12分)设数列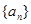 的前
的前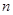 项和为
项和为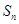 ,点
,点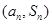 在直线
在直线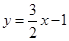 上.
上.
(Ⅰ)求数列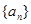 的通项公式;
的通项公式;
(Ⅱ)在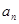 与
与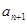 之间插入
之间插入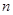 个数,使这
个数,使这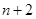 个数组成公差为
个数组成公差为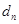 的等差数列,求数列
的等差数列,求数列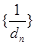 的前
的前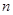 项和
项和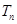 ,并求使
,并求使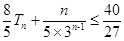 成立的正整数
成立的正整数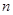 的最大值.
的最大值.
如图,已知四棱锥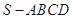 中,
中,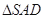 是边长为
是边长为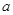 的正三角形,平面
的正三角形,平面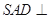 平面
平面 ,四边形
,四边形 是菱形,
是菱形,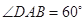 ,
,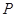 是
是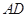 的中点,
的中点,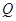 是
是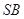 的中点.
的中点.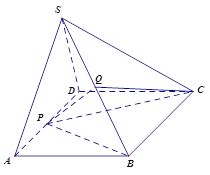
(Ⅰ)求证: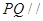 平面
平面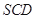 .
.
(Ⅱ)求二面角 的余弦值.
的余弦值.
【改编】在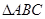 中,角
中,角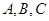 的对边分别为
的对边分别为 ,
,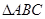 的外接圆半径
的外接圆半径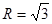 ,且满足
,且满足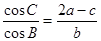 ,
,
(1)求角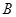 和边
和边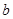 的大小;
的大小;
(2)若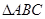 是锐角三角形,求
是锐角三角形,求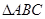 的面积的取值范围。
的面积的取值范围。