如图: PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=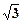 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.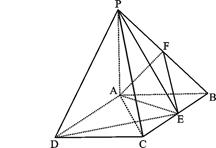
(Ⅰ)求三棱锥E-PAD的体积;
(Ⅱ)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(Ⅲ)证明:无论点E在边BC的何处,都有PE⊥AF.
已知函数 .
.
(Ⅰ)当a=1时,求曲线y=f(x0在x=1处的切线方程;
(Ⅱ)求函数f(x)在区间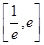 上的最小值;
上的最小值;
(Ⅲ)若关于 的方程
的方程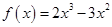 在区间
在区间 内有两个不相等的实数根,求实数a的取值范围.
内有两个不相等的实数根,求实数a的取值范围.
已知椭圆 (a>b>0)的两个焦点分别为
(a>b>0)的两个焦点分别为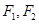 ,离心率为
,离心率为 ,过
,过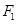 的直线l与椭圆C交于M,N两点,且
的直线l与椭圆C交于M,N两点,且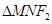 的周长为8.
的周长为8.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过原点O的两条互相垂直的射线与椭圆C分别交于A,B两点,证明:点O到直线AB的距离为定值,并求出这个定值.
已知数列 与
与 ,若
,若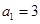 且对任意正整数
且对任意正整数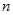 满足
满足 数列
数列 的前n项和
的前n项和 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前n项和
的前n项和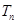 .
.
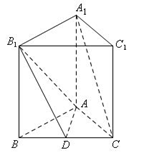
如图,正三棱柱(底面为正三角形,侧棱垂直于底面) 中,D是BC的中点,
中,D是BC的中点, .
.
(Ⅰ)求证: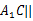 平面
平面 ;
;
(Ⅱ)求点C到平面 的距离.
的距离.
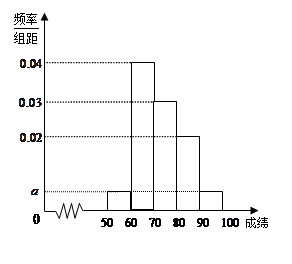
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是: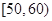 ,
,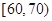 ,
,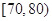 ,
,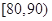 ,
,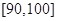 .
.
(Ⅰ)求图中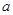 的值;
的值;
(Ⅱ)根据直方图,估计这100名学生语文成绩的平均分;
(Ⅲ)若这100名学生语文成绩某些分数段的人数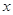 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数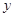 之比如下表所示,求数学成绩在
之比如下表所示,求数学成绩在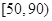 之外的人数.
之外的人数.
| 分数段 |
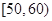 |
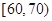 |
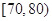 |
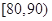 |
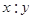 |
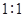 |
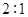 |
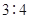 |
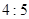 |