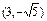
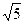
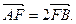
(1)求直线l的方程;
(2)求椭圆C的方程
(本小题满分12分)已知函数 .
.
(1)求 在区间[-2,1]上的最大值;
在区间[-2,1]上的最大值;
(2)若过点P(1,t)存在3条直线与曲线 相切,求t的取值范围;
相切,求t的取值范围;
(3)问过点A(-1,2),B(2,10),C(0,2)分别存在几条直线与曲线 相切?(只需写出结论)
相切?(只需写出结论)
(本小题满分12分)已知函数 =
= ,其中a∈R,且曲线y=
,其中a∈R,且曲线y= 在点(
在点(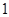 ,
,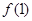 )处的切线垂直于直线
)处的切线垂直于直线 .
.
(1)求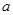 的值;
的值;
(2)求函数 的单调区间与极值.
的单调区间与极值.
(本小题满分12分)△ABC中,角A,B,C所对的边分别为a,b,c.已知a=3,cos A=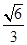 ,B=A+
,B=A+ .
.
(1)求b的值;
(2)求△ABC的面积.
(本小题满分12分)已知函数 .
.
(1)求 的值;
的值;
(2)求函数 的最小正周期及单调递增区间.
的最小正周期及单调递增区间.
(本小题满分12分)设命题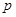 :实数
:实数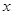 满足
满足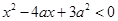 ,其中
,其中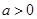 ,命题
,命题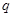 :实数
:实数 满足
满足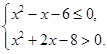 .
.
(1)若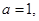 且
且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若 是
是
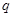 的充分不必要条件,求实数
的充分不必要条件,求实数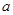 的取值范围.
的取值范围.