在正方体 中,
中, 分别是
分别是 中点.
中点.
(Ⅰ)求证:平面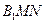 ⊥平面
⊥平面 ;
;
(Ⅱ)若在棱 上有一点
上有一点 ,使
,使 平面
平面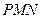 ,求
,求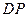 与
与 的比.
的比.
已知函数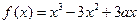
 在
在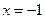 处,取得极值
处,取得极值
(1) 求实数 的值 (2) 求函数
的值 (2) 求函数 的单调区间,并指出其单调性。
的单调区间,并指出其单调性。
证明(1)已知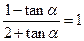 ,求证
,求证
(2)已知数列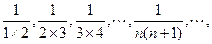 计算
计算 由此推算
由此推算 的公式,并用数学归纳法给出证明。
的公式,并用数学归纳法给出证明。
在棱长为 的正方体
的正方体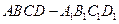 中,
中,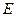 是线段
是线段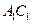 的中点,
的中点, .
.
(Ⅰ) 求证: ^
^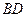 ;
;
(Ⅱ) 求证: ∥平面
∥平面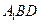 ;
;
(Ⅲ) 求三棱锥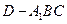 的体积.
的体积.
(本小题共14分)
已知函数
(1)试用含有a的式子表示b,并求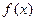 的单调区间;
的单调区间;
(2)设函数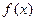 的最大值为
的最大值为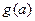 ,试证明不等式:
,试证明不等式:
(3)首先阅读材料:对于函数图像上的任意两点 ,如果在函数图象上存在点
,如果在函数图象上存在点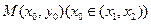 ,使得
,使得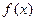 在点M处的切线
在点M处的切线 ,则称AB存在“相依切线”特别地,当
,则称AB存在“相依切线”特别地,当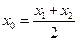 时,则称AB存在“中值相依切线”。
时,则称AB存在“中值相依切线”。
请问在函数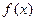 的图象上是否存在两点
的图象上是否存在两点 ,使得AB存在“中值相依切线”?若存在,求出一组A、B的坐标;若不存在,说明理由。
,使得AB存在“中值相依切线”?若存在,求出一组A、B的坐标;若不存在,说明理由。
(本小题共12分) 已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A、B的动点,且
已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A、B的动点,且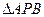 面积的最大值为
面积的最大值为
(1)求椭圆C的方程及离心率e; (2)直线AP与椭圆在点B处的切线交于点D,当直线AP绕点A
(2)直线AP与椭圆在点B处的切线交于点D,当直线AP绕点A 转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明。
转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明。