（本小题共12分）
已知A（-2，0），B（2，0）为椭圆C的左、右顶点，F为其右焦点，P是椭圆C上异于A、B的动点，且
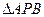面积的最大值为
（1）求椭圆C的方程及离心率e； （2）直线AP与椭圆在点B处的切线交于点D，当直线AP绕点A
转动时，试判断以BD为直径的圆与直线PF的位置关系，并加以证明。
(本题满分14分)
已知函数
．
(Ⅰ)求
的最大值及取得最大值时的
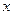集合；
(Ⅱ)设
的角
的对边分别为
，且
．求
的取值范围．
(本小题满分10分)
已知向量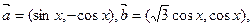
设函数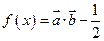
；
(1)写出函数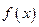
的单调递增区间；
(2)若x
求函数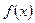
的最值及对应的x的值；-
(3)若不等式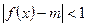
在x恒成立，求实数m的取值范围.
（本小题满分10分）
如图，在平面直角坐标系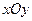
中，以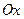
轴为始边做两个锐角
，它们的终边分别与单位圆相交于A、B两点，已知A、B的纵坐标分别为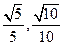
．
（1）求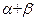
；
（2）求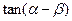
的值.
（本小题满分9分）
如图，在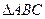
中，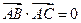
，
L为线段BC的垂直平分线，L与BC交与点D，E为L上异于D的任意一点，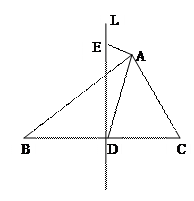
(1)求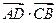
的值。
(2)判断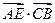
的值是否为一个常数，并说明理由。
（本小题满分9分）
已知：
（1）求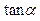
的值；
（2）求
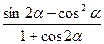的值．