已知动圆过定点P(1,0),且与定直线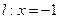 相切,点C在
相切,点C在 上.
上.
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且斜率为-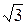 的直线与曲线M相交于A、B两点,
的直线与曲线M相交于A、B两点,
①求线段AB的长;
②问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由;
已知函数f(x)=ax2+bx+1(a,b为实数),x∈R,F(x)=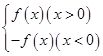
(1)若f(-1)=0,且函数f(x) ≥0的对任意x属于一切实数成立,求F(x)的表达式;
(2)在 (1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
在 中,
中,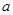 、
、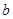 、
、 分别为角
分别为角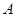 、
、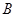 、
、 所对的边,角C是锐角,且
所对的边,角C是锐角,且 。
。
(1)求角 的值;
的值;
(2)若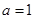 ,
, 的面积为
的面积为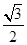 ,求
,求 的值。
的值。
在平面直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( ,
, 为参数),在以
为参数),在以 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 是圆心在极轴上,且经过极点的圆 已知曲线
是圆心在极轴上,且经过极点的圆 已知曲线 上的点
上的点 对应的参数
对应的参数 ,射线
,射线 与曲线
与曲线 交于点
交于点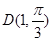
(1)求曲线 ,
, 的方程;
的方程;
(2)若点 ,
, 在曲线
在曲线 上,求
上,求 的值
的值
在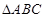 中,
中,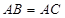 ,过点A的直线与其外接圆交于点P,交BC延长线于点D。
,过点A的直线与其外接圆交于点P,交BC延长线于点D。
(1)求证: ;
;
(2)若AC=3,求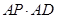 的值。
的值。
已知圆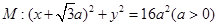 及定点
及定点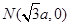 ,点
,点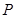 是圆
是圆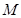 上的动点,点
上的动点,点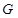 在
在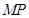 上,且满足
上,且满足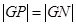 ,
,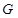 点的轨迹为曲线
点的轨迹为曲线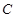 。
。
(1)求曲线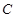 的方程;
的方程;
(2)若点 关于直线
关于直线 的对称点在曲线
的对称点在曲线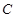 上,求
上,求 的取值范围。
的取值范围。