星体对它们的引力作用) .设四颗星稳定地分布在边长为 的正方形的四令顶点上且
的正方形的四令顶点上且
它们均围绕正方形对角线的交点做匀速圆周运动,星体运动周期为 ,每个星体表面
,每个星体表面
的重力加速度为g,引力常量为G,试求:每个星体的半径和质量.
一直立的气缸由截面积不同的两圆筒连接而成。质量均为1kg的活塞A、B用一长为2L的不可伸长的细绳连接,它们可在筒内无摩擦地上下滑动,A、B的截面积分别为SA=20cm2,SB=10cm2。A、B之间充有一定质量的理想气体,A的上方和B的下方都是大气,大气压始终保持为1.0×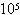 Pa。当气缸内气体温度为600升压强为12×
Pa。当气缸内气体温度为600升压强为12×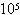 Pa时,活塞A、B的平衡位置如图所示。 当气缸内的气体温度由600k缓慢降低时,活塞A和B之间的距离保持不变,并一起向下缓慢移动(可认为两活塞仍处在平衡状态),直到活塞A移到两圆筒的连接处。若此后气体温度继续下降,求活塞A和B之间的距离开始小于2L时气体的温度。
Pa时,活塞A、B的平衡位置如图所示。 当气缸内的气体温度由600k缓慢降低时,活塞A和B之间的距离保持不变,并一起向下缓慢移动(可认为两活塞仍处在平衡状态),直到活塞A移到两圆筒的连接处。若此后气体温度继续下降,求活塞A和B之间的距离开始小于2L时气体的温度。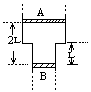
如图,A、B是两个汽缸,分别通过阀门a和b与压强为P0的大气相通,两个汽缸的横截面积之比SA∶SB=1∶10,中间的活塞D可无摩擦地左右滑动。区域C始终与大气相通。先关闭阀门a,再通过阀门b给气缸B充气至压强为PB=10P0,然后关闭b。①活塞D处于平衡状态时,汽缸A中气体压强PA多大?(设温度保持不变)②如果整个系统都升高到相同的温度,活塞将向哪个方向移动?为什么?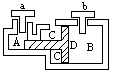
如图所示,一个圆筒形气缸平放在水平面上,A、B为两个可以无摩擦滑动的活塞,B活塞质量为m,A活塞的质量及厚度都可不计。B活塞用一根轻弹簧与气缸底相连,a、b为气缸侧壁上的两个小孔,与外界相通,两小孔及两活塞静止时的位置如左图所示。先用一根细管(细管容积不计)把a、b两孔连通,然后把气缸直立起来,并在A活塞上压一个质量也是m的砝码C,则B活塞下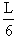 ,A活塞下降了
,A活塞下降了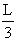 ,恰好挡住a孔,如右图所示。现在A活塞上再加一个与C相同的砝码D ,求A、B两活塞最后静止时的位置。(设温度始终保持不变)
,恰好挡住a孔,如右图所示。现在A活塞上再加一个与C相同的砝码D ,求A、B两活塞最后静止时的位置。(设温度始终保持不变) 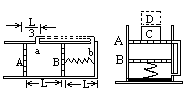
如图所示,一传热性能很好的容器两端是两个直径不同的两个圆筒,里面各有一个活塞,其截面积分别为 =10
=10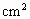 、
、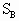 =4
=4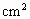 ,质量分别为
,质量分别为 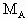 =6kg、
=6kg、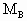 =4kG.它们之间用一质量不计的细杆相连,两活塞可在筒内无摩擦滑动但不漏气.在气温为-23℃时,用销子M把B栓住,并把阀门K打开,使容器与大气相通,随后关闭K,此时两活塞间体积为300
=4kG.它们之间用一质量不计的细杆相连,两活塞可在筒内无摩擦滑动但不漏气.在气温为-23℃时,用销子M把B栓住,并把阀门K打开,使容器与大气相通,随后关闭K,此时两活塞间体积为300 .当温度升至27℃时,将销子拔去,设大气压强
.当温度升至27℃时,将销子拔去,设大气压强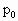 =1×
=1×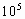 Pa,求:
Pa,求:
(1)刚拔去销子时,两活塞的加速度大小和方向;
(2)若活塞在各自圆筒内运动一段位移后速度达到最大,这段位移等于多少
如图所示,一定质量的气体放在体积为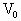 的容器中,室温为
的容器中,室温为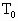 =300K,有一个光滑导热活塞C(不占体积)将容器分成A、B两室,B室的体积是A室体积的两倍,A室容器上连接有一个U形管(管内气体的体积忽略不计).两边水银柱高度差为76cm,右室容器连接有一个阀门K,可与大气相连通(外界大气压等于76cm汞柱)求:
=300K,有一个光滑导热活塞C(不占体积)将容器分成A、B两室,B室的体积是A室体积的两倍,A室容器上连接有一个U形管(管内气体的体积忽略不计).两边水银柱高度差为76cm,右室容器连接有一个阀门K,可与大气相连通(外界大气压等于76cm汞柱)求:
(1)将阀门K打开后,A室的体积变成多少?
(2)打开阀门K后将容器内的气体从300K分别加热到400K和500K,U形管内两边水银面的高度差各为多少?