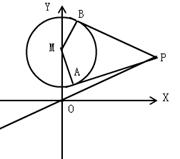
(本小题满分12分)如图, 已知圆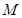 :
: 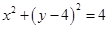 , 直线
, 直线 的方程为
的方程为 , 点
, 点 是直线
是直线 上一动点, 过点
上一动点, 过点 作圆的切线
作圆的切线 、
、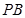 , 切点为
, 切点为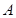 、
、 .
.
(1)当 的横坐标为
的横坐标为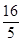 时, 求∠
时, 求∠ 的大小;
的大小;
(2)求证: 经过A、P、M三点的圆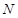 必过定点, 并求出所有定点的坐标.
必过定点, 并求出所有定点的坐标.
(本小题满分12分)标号为0到9的10瓶矿泉水.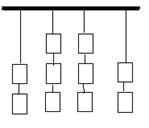
(1)从中取4瓶, 恰有2瓶上的数字相邻的取法有多少种?
(2)把10个空矿泉水瓶挂成如下4列的形式, 作为射击的靶子, 规定每次只能射击每列最下面的一个(射中后这个空瓶会掉到地下), 把10个矿泉水瓶全部击中有几种不同的射击方案?
(3)把击中后的矿泉水瓶分送给A、B、C三名垃圾回收人员, 每个瓶子1角钱.垃圾回收人员卖掉瓶子后有几种不同的收入结果?
(本小题满分12分)下图是调查某地某公司1000名员工的月收入后制作的直方图.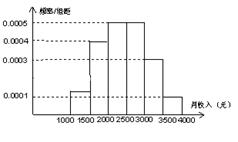
(1)求该公司员工的月平均收入及员工月收入的中位数;
(2)在收入为1000至1500元和收入为3500至4000元的员工中用分层抽样的方法抽取一个容量15的样本, 员工甲、乙的月收入分别为1200元、3800元, 求甲乙同时被抽到的概率.
函数 对于任意的实数
对于任意的实数 都有
都有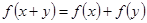 成立,且当
成立,且当 时
时 恒成立.
恒成立.
(1)证明函数 的奇偶性;
的奇偶性;
(2)若 ,求函数
,求函数 在
在 上的最大值;
上的最大值;
(3)解关于 的不等式
的不等式
已知定义域为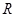 的函数
的函数 是奇函数.
是奇函数.
(1)求 的值;
的值;
(2)若对任意的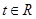 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.