(本小题满分12分)标号为0到9的10瓶矿泉水.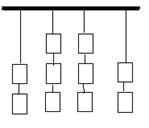
(1)从中取4瓶, 恰有2瓶上的数字相邻的取法有多少种?
(2)把10个空矿泉水瓶挂成如下4列的形式, 作为射击的靶子, 规定每次只能射击每列最下面的一个(射中后这个空瓶会掉到地下), 把10个矿泉水瓶全部击中有几种不同的射击方案?
(3)把击中后的矿泉水瓶分送给A、B、C三名垃圾回收人员, 每个瓶子1角钱.垃圾回收人员卖掉瓶子后有几种不同的收入结果?
(本小题满分14分)
直线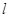 与椭圆
与椭圆 交于
交于 ,
, 两点,已知
两点,已知
 ,
,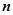
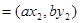 ,若
,若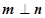 且椭圆的离心率
且椭圆的离心率 ,又椭圆经过点
,又椭圆经过点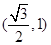 ,
,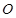 为坐标原点.
为坐标原点.
(1)求椭圆的方程;
(2)若直线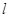 过椭圆的焦点
过椭圆的焦点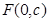 (
( 为半焦距),求直线
为半焦距),求直线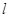 的斜率
的斜率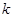 的值;
的值;
(3)试问: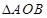 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
(本小题满分12分)
已知函数
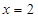 是
是 的一个极值点.
的一个极值点.
(1)求函数 的单调区间;
的单调区间;
(2)若当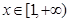 时,
时, 恒成立,求
恒成立,求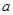 的取值范围.
的取值范围.
如图,在梯形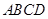 中,
中,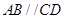 ,
,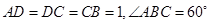 ,四边形
,四边形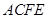 为矩形,平面
为矩形,平面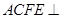 平面
平面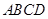 ,
, .
.
(1)求证: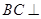 平面
平面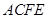 ;
;
(2)点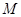 在线段
在线段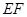 上运动,设平面
上运动,设平面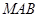 与平面
与平面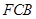 所成二面角的平面角为
所成二面角的平面角为 ,试求
,试求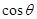 的取值范围.
的取值范围.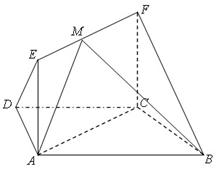
(本小题满分12分)
在一次数学考试中,第21题和第22题为选做题. 规定每位考生必须且只须在其中选做一题. 设4名考生选做这两题的可能性均为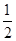 .
.
(1)求其中甲、乙二名学生选做同一道题的概率;
(2)设这4名考生中选做第22题的学生个数为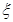 ,求
,求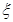 的概率分布及数学期望.
的概率分布及数学期望.
(本小题满分12分)
已知数列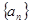 是公差为2的等差数列,且
是公差为2的等差数列,且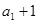 ,
,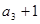 ,
,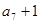 成等比数列.
成等比数列.
(1)求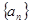 的通项公式;
的通项公式;
(2)令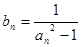
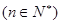 ,记数列
,记数列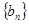 的前
的前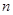 项和为
项和为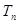 ,求证:
,求证: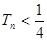 .
.