设椭圆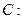
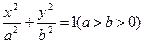的离心率为
=
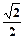,点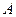
是椭圆上的一点,且点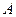到椭圆
两焦点的距离之和为4.
(1)求椭圆的方程；
（2）椭圆上一动点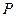
关于直线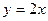
的对称点为
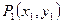,求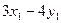
的取值范围.
（m为常数，且m>0）有极大值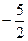
，
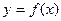的斜率为2的切线方程．
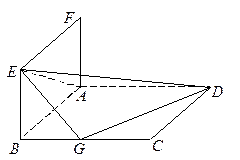
的正切值．
件，每个元件的库存费为每年2元，如果不计其他费用，请你帮公司计算，每年进货几次花费最小？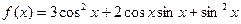
．
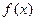的单调递增区间．
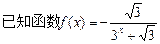
(1)求证：函数y=f(x)的图象关于点（0.5，－0.5）对称；
(2)求f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)的值;