已知向量 ,
, .
.
(Ⅰ)若 ,求函数
,求函数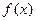 关于
关于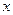 的解析式;
的解析式;
(Ⅱ)求(1)中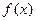 的单调递减区间;
的单调递减区间;
已知椭圆 过
过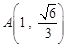 和点
和点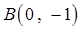 .
.
(1)求椭圆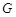 的方程;
的方程;
(2)设过点 的直线
的直线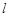 与椭圆
与椭圆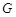 交于
交于 两点,且
两点,且 ,求直线
,求直线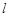 的方程.
的方程.
如图,四棱锥 的底面
的底面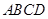 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中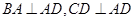 ,
, ,平面
,平面 底面
底面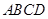 ,
,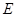 是
是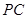 的中点.
的中点.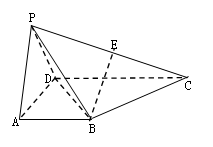
(1)求证: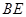 //平面
//平面 ;
;
(2)求证: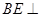
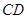 ;
;
(3)求三棱锥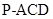 的体积
的体积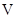 .
.
从某校高三上学期期末数学考试成绩中,随机抽取了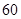 名学生的成绩得到频率分布直方图如下图所示:
名学生的成绩得到频率分布直方图如下图所示: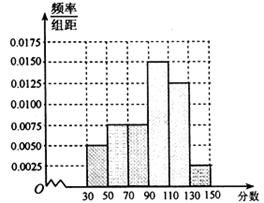
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分(平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和);
(2)若用分层抽样的方法从分数在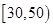 和
和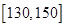 的学生中共抽取
的学生中共抽取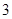 人,该
人,该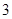 人中成绩在
人中成绩在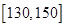 的有几人?
的有几人?
(3)在(2)中抽取的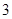 人中,随机抽取
人中,随机抽取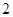 人,求分数在
人,求分数在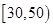 和
和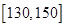 各
各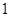 人的概率.
人的概率.
已知函数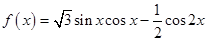 ,
,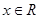 .
.
(1)求函数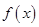 的最小正周期;
的最小正周期;
(2)在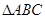 中,角
中,角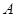 、
、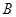 、
、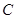 的对边分别为
的对边分别为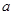 、
、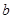 、
、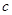 ,且满足
,且满足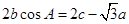 ,
,
求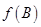 的值.
的值.
设 (
( ,
, ),
), (
( ,
, )是函数
)是函数 的图象上的任意两点.
的图象上的任意两点.
(1)当 时,求
时,求 +
+ 的值;
的值;
(2)设 ,其中
,其中 ,求
,求
(3)对应(2)中 ,已知
,已知 ,其中
,其中 ,设
,设 为数列
为数列 的前
的前 项和,求证
项和,求证 .
.