如图,四棱锥 的底面
的底面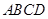 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中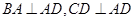 ,
, ,平面
,平面 底面
底面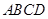 ,
,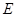 是
是 的中点.
的中点.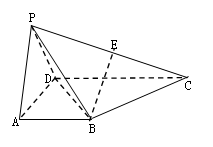
(1)求证: //平面
//平面 ;
;
(2)求证:
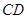 ;
;
(3)求三棱锥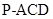 的体积
的体积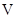 .
.
(本小题满分12分)高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 |
频数 |
频率 |
 |
① |
② |
 |
0.050 |
|
 |
0.200 |
|
 |
12 |
0.300 |
 |
0.275 |
|
 |
4 |
③ |
 |
0.050 |
|
| 合 计 |
④ |
(1)根据上面图表,①、② 、③、④处的数值分别是多少?
、③、④处的数值分别是多少?
(2)在坐标系中画出 的频率分布直方图;
的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在 中的概率。
中的概率。
(本小题满分12分)已知命题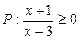 ,命题
,命题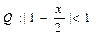 ,若
,若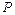 是真命题,
是真命题,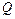 是假命题,求实数
是假命题,求实数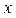 的取值范围。
的取值范围。
已知双曲线C的中心是原点,右焦点为F( ,0),一条渐近线m:x+
,0),一条渐近线m:x+ y=0,设过点A(-3
y=0,设过点A(-3 ,0)的直线l
,0)的直线l
(1)求双曲线C的方程;
(2)若过原点的直线a∥l,且a与l的距离为 ,求k的值;
,求k的值;
(3)证明:当k> 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为 .
.
过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线l作垂线,垂足分别为M1、N1.
(1)求证:FM1⊥FN1;
(2)记△FMM1、△FM1N1、△FNN1的面积分别为 、
、 、
、 ,试判断S
,试判断S =4
=4
 是否成立,并证明你的结论.
是否成立,并证明你的结论.
如图,已知椭圆 =1(a>b>0)过点(1,
=1(a>b>0)过点(1, ),离心率为
),离心率为 ,左、右焦点分别为F1、F2. 点P为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.
,左、右焦点分别为F1、F2. 点P为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.
(1)求椭圆的标准方程;
(2)设直线PF1、PF2的斜率分别为k1、k2, 证明: =2;
=2;