在一次考试中共有８道选择题，每道选择题都有４个选项，其中有且只有一个选项是正确的．评分标准规定：“每题只选一个选项，选对得５分，不选或选错得０分”．某考生已确定有4道题答案是正确的，其余题中：有两道只能分别判断２个选项是错误的，有一道仅能判断１个选项是错误的，还有一道因不理解题意只好乱猜，求：
（１）该考生得40分的概率；
（２）该考生得多少分的可能性最大？
（３）该考生所得分数的数学期望．
已知数列{an}、{bn}满足：a1=1，a2=a（a为实数），且
，其中n=1，2，3，…
（Ⅰ）求证：“若数列{an}是等比数列，则数列{bn}也是等比数列”是真命题；
（Ⅱ）写出（Ⅰ）中命题的逆命题；判断它是真命题还是假命题，并说明理由.
设全集
，函数
的定义域为A,函数
的定义域为B
(Ⅰ)求集合
与
；
(Ⅱ)求
、
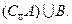
给定项数为
的数列
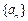，其中
.
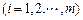若存在一个正整数
，若数列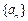中存在连续的k项和该数列中另一个连续的k项恰好按次序对应相等，则称数列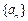是“k阶可重复数列”，
例如数列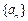
因为
与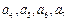
按次序对应相等，所以数列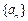是“4阶可重复数列”.
（Ⅰ）分别判断下列数列
①
②
是否是“5阶可重复数列”？如果是，请写出重复的这5项；
（Ⅱ）若数为的数列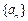一定是 “3阶可重复数列”，则的最小值是多少？说明理由；
（III）假设数列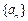不是“5阶可重复数列”，若在其最后一项
后再添加一项0或1，均可使新数列是“5阶可重复数列”，且
，求数列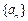的最后一项的值.
一束光线从点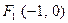
出发，经直线
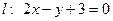上一点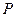
反射后，恰好穿过点
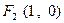．（Ⅰ）求点
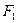关于直线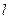
的对称点
的坐标；
（Ⅱ）求以、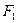
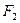为焦点且过点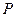的椭圆
的方程；
（Ⅲ）设直线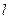与椭圆的两条准线分别交于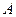
、
两点，点
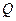为线段
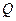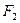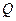上的动点，求点到的距离与到椭圆右准线的距离之比的最小值，并求取得最小值时点的坐标．
