已知函数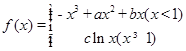 的图像在点
的图像在点 处的切线方程为
处的切线方程为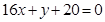 .
.
(Ⅰ)求实数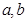 的值;
的值;
(Ⅱ)求函数 在区间
在区间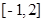 上的最大值;
上的最大值;
(Ⅲ)若曲线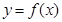 上存在两点
上存在两点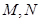 使得
使得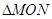 是以坐标原点
是以坐标原点 为直角顶点的直角三角形,且斜边
为直角顶点的直角三角形,且斜边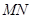 的中点在
的中点在 轴上,求实数
轴上,求实数 的取值范围.
的取值范围.
设椭圆中心在坐标原点,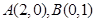 是它的两个顶点,直线
是它的两个顶点,直线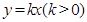 与直线
与直线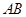 相交于点D,与椭圆相交于
相交于点D,与椭圆相交于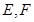 两点.
两点.
(Ⅰ)若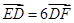 ,求
,求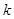 的值;
的值;
(Ⅱ)求四边形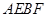 面积的最大值.
面积的最大值.
由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高,然而也有部分公众对该活动的实际效果与负面影响提出了疑问,对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| 支持 |
保留 |
不支持 |
|
| 20岁以下 |
800 |
450 |
200 |
| 20岁以上(含20岁) |
100 |
150 |
300 |
(Ⅰ)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从持“支持”态度的人中抽取了45人,求n的值;
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中任意选取2人,求至少有1人20岁以下的概率;
(Ⅲ)在接受调查的人中,有8人给这项活动打出的分数如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8个人打出的分数看作一个总体,从中任取1个数,求该数与总体平均数之差的绝对值超过0.6的概率.
在如图所示的几何体中,四边形 是正方形,
是正方形,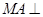 平面
平面 ,
, ,
, 分别为
分别为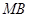 ,
,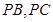 的中点,且
的中点,且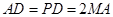 .
.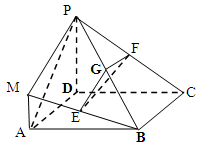
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求三棱锥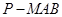 与四棱锥
与四棱锥 的体积之比.
的体积之比.
南充市某广场有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为 ,
, ,经测量
,经测量 米,
米, 米,
米, 米,
米,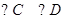 .
.
(Ⅰ)求 的长度;
的长度;
(Ⅱ)若环境标志的底座每平方米造价为5000元,不考虑其他因素,小李、小王谁的设计使建造费用最低(请说明理由)?最低造价为多少?(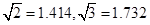 )
)