南充市某广场有一块不规则的绿地如图所示，城建部门欲在该地上建造一个底座为三角形的环境标志，小李、小王设计的底座形状分别为
，
，经测量
米，
米，
米，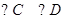
.
（Ⅰ）求
的长度；
（Ⅱ）若环境标志的底座每平方米造价为5000元，不考虑其他因素，小李、小王谁的设计使建造费用最低（请说明理由）？最低造价为多少？（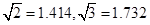
）
已知等比数列{an}中，a3=
,S3=4
,求a1.
某林场有荒山3 250亩，每年春季在荒山上植树造林，第一年植树100亩，计划每年比上一年多植树50亩（全部成活）
（1）问需要几年，可将此山全部绿化完？
（2）已知新种树苗每亩的木材量是2立方米，树木每年自然增长率为10%，设荒山全部绿化后的年底的木材总量为S.求S约为多少万立方米？（精确到0.1）
在等比数列{an}中，a1+a2+a3+a4+a5=8且
+
+
+
+
=2,求a3.
已知数列{an}的前n项和为Sn，且对任意n∈N*有an+Sn=n.
（1）设bn=an-1,求证：数列{bn}是等比数列；
（2）设c1=a1且cn=an-an-1 (n≥2)，求{cn}的通项公式.
已知{an}为等比数列，a3=2，a2+a4=
，求{an}的通项公式.