已知在等比数 列
列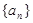 中,
中,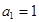 ,且
,且 是
是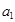 和
和 的等差中项.
的等差中项.
(1 )求数列
)求数列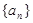 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,求
,求 的前
的前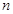 项和
项和 .
.
已知:A、B、C是 的内角,
的内角,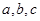 分别是其对边长,向量
分别是其对边长,向量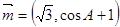 ,
, ,且
,且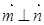 .
.
(1)求角A的大小;(2)若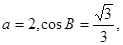 求
求 的长
的长
已知二次函数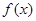 满足:①当
满足:①当 时有极值,②图象与y轴交点的纵坐标为
时有极值,②图象与y轴交点的纵坐标为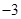 ,且在该点处的切线与直线
,且在该点处的切线与直线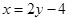 垂直
垂直
(I)求f(1)的值
(II)求函数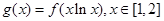 的值域
的值域
(III)若曲线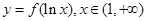 上任意一点处的切线的斜率恒大于
上任意一点处的切线的斜率恒大于 ,求
,求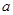 的取值范围
的取值范围
如图,线段AB的两个端点A、B分别在x轴,y轴上滑动,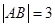 ,点M是线段
,点M是线段
AB上一点,且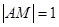 点M随线段AB的滑动而运动。
点M随线段AB的滑动而运动。
(I)求动点M的轨迹E的方程
(II)过定点N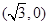 的直线
的直线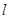 交曲线E于C、D两点,交y轴于点P,若
交曲线E于C、D两点,交y轴于点P,若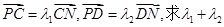 的值
的值
如图,在多面体ABCD中,DB⊥平面ABC,AE∥BD,且AB=BC=CA=BD=2AE=2
(I)求证:平面ECD⊥平面BCD
(II)求二面角D-EC-B的正切值
(III)求三棱锥A-ECD的体积