求下列函数的单调区间:
在数列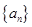 中,已知
中,已知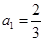 ,
,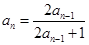 .
.
(1)求 、
、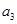 并判断
并判断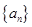 能否为等差或等比数列;
能否为等差或等比数列;
(2)令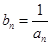 ,求证:
,求证: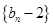 为等比数列;
为等比数列;
(3)求数列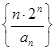 的前n项和
的前n项和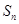 .
.
若定义在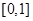 上的函数
上的函数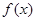 同时满足:①
同时满足:①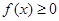 ;②
;②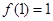 ;③若
;③若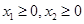 ,且
,且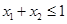 ,则
,则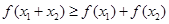 成立.则称函数
成立.则称函数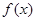 为“梦函数”.
为“梦函数”.
(1)试验证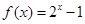 在区间
在区间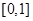 上是否为“梦函数”;
上是否为“梦函数”;
(2)若函数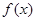 为“梦函数”,求
为“梦函数”,求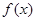 的最值.
的最值.
如图,在三棱锥A-BCD中,平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点,且MN=PQ.
(1)求证:四边形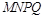 为平行四边形;
为平行四边形;
(2)试在直线AC上找一点F,使得 .
.
学校为了预防甲流感,每天上午都要对同学进行体温抽查。某一天,随机抽取甲、乙两个班级各10名同学,测量他们的体温如图:(单位0.1℃)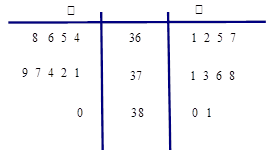
(1)哪个班所选取的这10名同学的平均体温高?
(2)一般 ℃为低热,
℃为低热,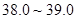 ℃为中等热,
℃为中等热,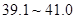 ℃为高热。按此规定,记事件A为“从甲班发热的同学中任选两人,有中等热的同学”,记事件B为“从乙班发热的同学中任选两人,有中等热的同学”,分别求事件A和事件B的概率.
℃为高热。按此规定,记事件A为“从甲班发热的同学中任选两人,有中等热的同学”,记事件B为“从乙班发热的同学中任选两人,有中等热的同学”,分别求事件A和事件B的概率.
已知 ,函数
,函数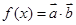 .
.
(1)求 的最值和单调递减区间;
的最值和单调递减区间;
(2)已知在△ABC中,角A、B、C的对边分别为 ,
, ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.