证明:若函数 在点
在点 处可导,则函数
处可导,则函数 在点
在点 处连续.
处连续.
个是趋向的转化,另一个是形式(变为导数定义形式)的转化.
(本小题12分) 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,
且∠A1AD=∠A1AB=60°。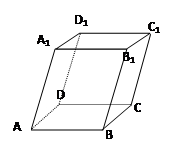
①求证四棱锥 A1-ABCD为正四棱锥;
②求侧棱AA1到截面B1BDD1的距离;
③求侧面A1ABB1与截面B1BDD1的锐二面角大小。
(本小题12分) 正项数列{an}满足a1=2,点An(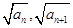 )在双曲线y2-x2=1上,点(
)在双曲线y2-x2=1上,点( )在直线y=-
)在直线y=-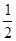 x+1上,其中Tn是数列{bn}的前n项和。
x+1上,其中Tn是数列{bn}的前n项和。
①求数列{an}、{bn}的通项公式;
②设Cn=anbn,证明 Cn+1<Cn
③若m-7anbn>0恒成立,求正整数m的最小值。
(本小题12分) 某工厂组织工人参加上岗测试,每位测试者最多有三次机会,一旦某次测试通过,便可上岗工作,不再参加以后的测试;否则就一直测试到第三次为止。设每位工人每次测试通过的概率依次为0.2,0.5,0.5,每次测试相互独立。
(1)求工人甲在这次上岗测试中参加考试次数为2、3的概率分别是多少?
(2)若有4位工人参加这次测试,求至少有一人不能上岗的概率。
(本小题12分)  =(
=( ),
),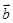 =
=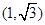 ,f(x)=
,f(x)=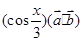
①求f(x)图象对称中心坐标
②若△ABC三边a、b、c满足b2=ac,且b边所对角为x,求x的范围及f(x)值域。
已知函数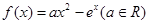 .
.
(Ⅰ)当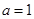 时,试判断
时,试判断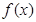 的单调性并给予证明;
的单调性并给予证明;
(Ⅱ)若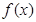 有两个极值点
有两个极值点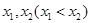 .
.
(i) 求实数a的取值范围;
(ii)证明: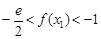 。 (注:
。 (注: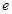 是自然对数的底数)
是自然对数的底数)