甲乙两公司生产同一种新产品,经测算,对于函数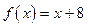 ,
, ,及任意的
,及任意的 ,当甲公司投入
,当甲公司投入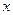 万元作宣传时,乙公司投入的宣传费若小于
万元作宣传时,乙公司投入的宣传费若小于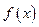 万元,则乙公司有失败的危险,否则无失败的危险;当乙公司投入
万元,则乙公司有失败的危险,否则无失败的危险;当乙公司投入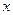 万元作宣传时,甲公司投入的宣传费若小于
万元作宣传时,甲公司投入的宣传费若小于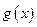 万元,则甲公司有失败的危险,否则无失败的危险. 设甲公司投入宣传费x万元,乙公司投入宣传费y万元,建立如图直角坐标系,试回答以下问题:
万元,则甲公司有失败的危险,否则无失败的危险. 设甲公司投入宣传费x万元,乙公司投入宣传费y万元,建立如图直角坐标系,试回答以下问题:
(1)请解释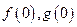 ;
;
(2)甲、乙两公司在均无失败危险的情况下尽可能少地投入宣传费用,问此时各应投入多少宣传费?
(3)若甲、乙分别在上述策略下,为确保无失败的危险,根据对方所投入的宣传费,按最少投入费用原则,投入自己的宣传费:若甲先投入 万元,乙在上述策略下,投入最少费用
万元,乙在上述策略下,投入最少费用 ;而甲根据乙的情况,调整宣传费为
;而甲根据乙的情况,调整宣传费为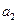 ;同样,乙再根据甲的情况,调整宣传费为
;同样,乙再根据甲的情况,调整宣传费为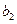
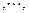 如此得当甲调整宣传费为
如此得当甲调整宣传费为 时,乙调整宣传费为
时,乙调整宣传费为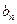 ;试问是否存在
;试问是否存在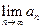 ,
,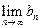 的值,若存在写出此极限值(不必证明),若不存在,说明理由.
的值,若存在写出此极限值(不必证明),若不存在,说明理由.
(本小题满分14分)在平面直角坐标系中,已知点 ,过点
,过点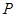 作抛物线
作抛物线 的切线,其切点分别为
的切线,其切点分别为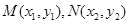 (其中
(其中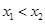 )。
)。
⑴ 求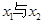 的值;
的值;
⑵ 若以点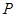 为圆心的圆与直线
为圆心的圆与直线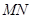 相切,求圆的面积。
相切,求圆的面积。
(本小题满分14分)如图,在长方体 中,
中, ,
,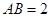 ,点
,点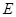 在棱
在棱 上移动.
上移动.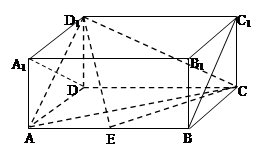
⑴ 证明: //平面
//平面 ;
;
⑵证明: ⊥
⊥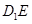 ;
;
⑶ 当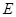 为
为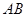 的中点时,求四棱锥
的中点时,求四棱锥 的体积.
的体积.
(本小题满分12分)为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.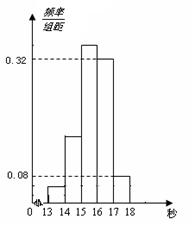
⑴将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
⑵求调查中随机抽取了多少个学生的百米成绩;
⑶若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.
(本小题满分12分) 已知向量 ,
,
⑴求函数 的最小正周期;
的最小正周期;
⑵若 ,求函数
,求函数 的单调递增区间.
的单调递增区间.
(本小题满分14分)
已知数列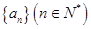 满足:
满足: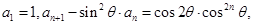 其中
其中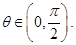
(1)当 时,求
时,求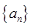 的通项公式;
的通项公式;
(2)在(1)的条件下,若数列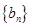 中,
中,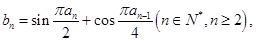 且
且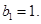 求证:对于
求证:对于 恒成立;
恒成立;
(3)对于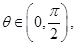 设
设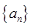 的前
的前 项和为
项和为 ,试比较
,试比较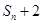 与
与 的大小.
的大小.