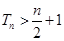将两颗骰子先后各抛一次,a,b表示抛甲、乙两颗骰子所得的点数.(Ⅰ)若点(a,b)落在不等式组表示的平面区域内的事件记为A,求事件A的概率;(Ⅱ)若点(a,b)落在直线x+y=m上,且使此事件的概率最大,求m的值.
(本小题满分12分)已知函数
(1)求函数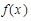 的最小正周期及在
的最小正周期及在 单调递增区间;
单调递增区间;
(2)在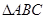 中,A、B、C分别为三边
中,A、B、C分别为三边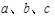 所对的角,若
所对的角,若 ,求
,求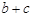 的最大值.
的最大值.
(本小题满分12分)已知某校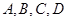 四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从
四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从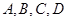 四个社团的学生当中随机抽取10名学生参加问卷调查.
四个社团的学生当中随机抽取10名学生参加问卷调查.
(Ⅰ)从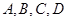 四个社团中各抽取多少人?
四个社团中各抽取多少人?
(Ⅱ)在社团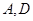 所抽取的学生总数中,任取2个,求
所抽取的学生总数中,任取2个,求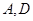 社团中各有1名学生的概率.
社团中各有1名学生的概率.
(本小题满分14分)已知函数 (
( 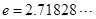 是自然对数的底数),
是自然对数的底数), .
.
(1)若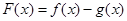 ,求
,求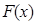 的极值;
的极值;
(2)对任意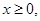 证明:
证明: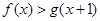 ;
;
(3)对任意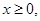 都有
都有 成立,求实数
成立,求实数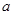 的取值范围.
的取值范围.
(本小题满分13分)已知椭圆 ,其中
,其中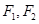 为左、右焦点,O为坐标原点.直线l与椭圆交于
为左、右焦点,O为坐标原点.直线l与椭圆交于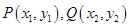 两个不同点.当直线l过椭圆C右焦点F2且倾斜角为
两个不同点.当直线l过椭圆C右焦点F2且倾斜角为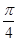 时,原点O到直线l的距离为
时,原点O到直线l的距离为 .又椭圆上的点到焦点F2的最近距离为
.又椭圆上的点到焦点F2的最近距离为 .
.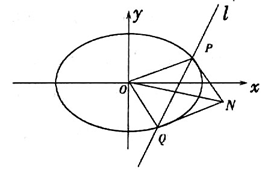
(1)求椭圆C的方程;
(2)以OP,OQ为邻边做平行四边形OQNP,当平行四边形OQNP面积为 时,求平行四边形OQNP的对角线之积
时,求平行四边形OQNP的对角线之积 的最大值;
的最大值;
(3)若抛物线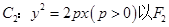 为焦点,在抛物线C2上任取一点S(S不是原点O),以OS为直径作圆,交抛物线C2于另一点R,求该圆面积最小时点S的坐标.
为焦点,在抛物线C2上任取一点S(S不是原点O),以OS为直径作圆,交抛物线C2于另一点R,求该圆面积最小时点S的坐标.
(本小题满分12分)已知 是等差数列
是等差数列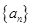 的前n项和,数列
的前n项和,数列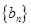 是等比数列,
是等比数列, 恰为
恰为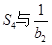 的等比中项,圆
的等比中项,圆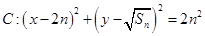 ,直线
,直线 ,对任意
,对任意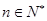 ,直线
,直线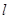 都与圆C相切.
都与圆C相切.
(Ⅰ)求数列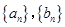 的通项公式;
的通项公式;
(Ⅱ)若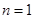 时,
时,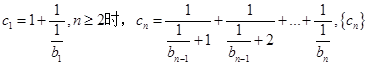 的前n项和为
的前n项和为 ,求证:对任意
,求证:对任意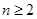 ,都有
,都有