如图,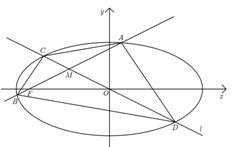
已知椭圆E: 的离心率为
的离心率为 ,过左焦点
,过左焦点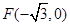 且斜率为
且斜率为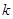 的直线交
的直线交
椭圆E于A,B两点,线段AB的中点为M,直线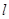 :
: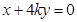 交椭圆E于C,D两点.
交椭圆E于C,D两点.
(1)求椭圆E的方程;
(2)求证:点M在直线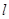 上;
上;
(3)是否存在实数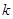 ,使得四边形AOBC为平行四边形?若存在求出
,使得四边形AOBC为平行四边形?若存在求出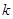 的值,若不存在说明理
的值,若不存在说明理
由.
已知曲线
 .
.
(1)求曲线在点( )处的切线方程;
)处的切线方程;
(2)若存在 使得
使得 ,求
,求 的取值范围.
的取值范围.
如图,四边形ABCD与四边形 都为正方形,
都为正方形, ,F
,F
为线段 的中点,E为线段BC上的动点.
的中点,E为线段BC上的动点.
(1)当E为线段BC中点时,求证: 平面AEF;
平面AEF;
(2)求证:平面AEF
 平面;
平面;
(3)设 ,写出
,写出 为何值时MF⊥平面AEF(结论不要求证明).
为何值时MF⊥平面AEF(结论不要求证明).
年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人,他们的健康状况如下表:
其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,-1代表“生活不能自理”。
(1)随机访问该小区一位80岁以下的老龄人,该老人生活能够自理的概率是多少?
(2)按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位.求被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率.
已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 在区间
在区间 上的最小值和最大值.
上的最小值和最大值.