圆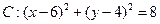
上一点A(4，6)作圆的一条动弦AB，点P为弦AB的中点.
（Ⅰ）求点P的轨迹方程；
（Ⅱ）设点P关于点D(9，0)的对称点为E，O为坐标原点，将线段OP绕原点O依逆时针方向旋转90°后，所得线段为OF，求|EF|的取值范围.
选修4－1：几何证明选讲如图，已知AD是△ABC的外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连结FB、FC.
（Ⅰ）求证：FB=FC；
（Ⅱ）求证：FB2=FA·FD；
（本小题满分12分）已知函数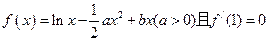
,
（Ⅰ）试用含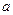
的式子表示b，并求函数
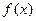的单调区间；
（Ⅱ）已知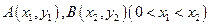
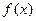为函数图象上不同两点，
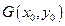为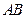
的中点，记AB两点连线斜率为K，证明：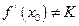
已知椭圆
的离心率
，短轴长为
.
（Ⅰ）求椭圆方程；（Ⅱ）若椭圆与
轴正半轴、
轴正半轴的交点分别为
、
，经过点
且斜率为
的直线
与椭圆交于不同的两点
、
．是否存在常数，使得向量
共线？如果存在，求的值；如果不存在，请说明理由．
（本小题满分12分）已知等差数列
为递增数列，且
是方程
的两根，数列
的前
项和
；
（1）求数列和的通项公式；
（2）若
，
为数列
的前n项和，证明：
已知二次函数
为偶函数，
函数
的图象与直线
相切．
（1）求的解析式；
（2）若函数
上是单调减函数，那么：
①求
的取值范围；
②是否存在区间
，使得在区间
上的值域恰好为
？若存在，请求出区间[m，n]；若不存在，请说明理由．