已知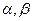
都是锐角，且
．
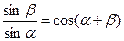（Ⅰ）求证：
；
（Ⅱ）当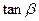
取最大值时，求
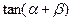的值．
（本题14分）
已知函数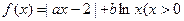
，实数a，b为常数），
（1）若a＝1，
在（0，＋∞）上是单调增函数，求b的取值范围；
（2）若a≥2，b＝1，求方程
在（0，1]上解的个数。
（本题12分）已知中心为坐标原点O，焦点在x轴上的椭圆的两个短轴端点和左右焦点所组成的四边形是面积为2的正方形，
（1）求椭圆的标准方程；
（2）过点P（0，2）的直线l与椭圆交于点A，B，当△OAB面积最大时，求直线l的方程。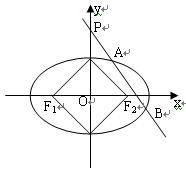
（本题12分）已知数列{an}的前n项和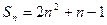
，数列{bn}满足b1＋3b2＋…＋（2n－1）b
n＝（2n―3）·2n＋1，
求：数列{anbn}的前n项和Tn。
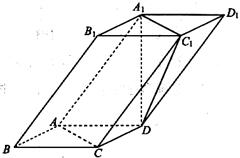
（本题12分）如图，四棱柱ABCD—A
BCD中，AD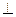
平面ABCD，底面ABCD是边长为1的正方形，侧棱AA=2．
（1）求证：CD∥平面ABBA；
（2）求直线BD与平面ACD所成角的正弦值；
（3）求二面角D—AC一A的余弦值．
）的定义域、值域，并指出它的周期、奇偶性和单调性