(本小题满分13分)甲、乙、丙三人参加了一家公司招聘面试,甲表示只要面试合格就签约;乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约,设每人面试合格的概率都是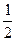 ,且面试是否合格互不影响。(1)求至少有一人面试合格的概率;(2)求签约人数
,且面试是否合格互不影响。(1)求至少有一人面试合格的概率;(2)求签约人数 的分布列和数学期望;
的分布列和数学期望;
若数列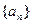 的前
的前 项和为
项和为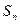 ,点
,点 均在函数
均在函数 的图象上
的图象上
(1)求数列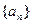 的通项公式;
的通项公式;
(2)若数列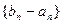 是首项为1,公比为
是首项为1,公比为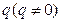 的等比数列,求数列
的等比数列,求数列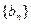 的前
的前 项和
项和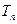 .
.
、如图,已知四棱锥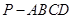 中,底面
中,底面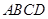 是直角梯形,
是直角梯形, ,
,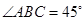 ,
,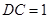 ,
,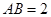 ,
, 平面
平面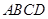 ,
,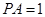 .
.
(1)求证: 平面
平面 ;
;
(2)求证: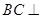 平面
平面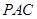 ;
;
(3)若M是PC的中点,求三棱锥M—ACD的体积.
已知函数 (
(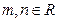 )在
)在 时有极值,其图象在点
时有极值,其图象在点 处的切线与直线
处的切线与直线 平行。
平行。
(1)求m,n的值; (2)求函数 的单调区间。
的单调区间。
某工厂有A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天8h计算,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
在△ABC中,已知B=45°,D是BC边上的一点,AB=5
 ,AC="14," DC=6,求AD的长.
,AC="14," DC=6,求AD的长.