某工厂有A、B两种配件生产甲、乙两种产品，每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h，该厂每天最多可从配件厂获得16个A配件和12个B配件，按每天8h计算，若生产一件甲产品获利2万元，生产一件乙产品获利3万元，采用哪种生产安排利润最大？
过点P（－3，0）且倾斜角为30°的直线和曲线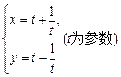
相交于A、B两点．求线段AB的长．
已知一四棱锥P－ABCD的三视图如下，E是侧棱PC上的动点。
(Ⅰ)求四棱锥P－ABCD的体积；
（Ⅱ）是否不论点E在何位置，都有BD⊥AE？证明你的结论;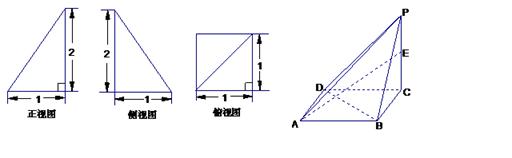
如图是一个空间几何体的三视图，其中正视图和侧视图都是边长为2的正三角形，俯视图是一个正方形．
（Ⅰ）在给定的空间直角坐标系中作出这个几何体的直观图(不用写作法)；
（Ⅱ）求这个几何体的体积．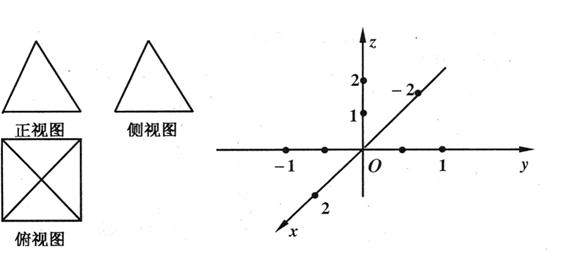
一个简单多面体的直观图和三视图如图所示，它的主视图和侧视图都是腰长为1的等腰直角三角形，俯视图为正方形，E是PD的中点.
（1）求证: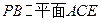
；
（2）求证:
；
（3）求三棱锥
的体积.
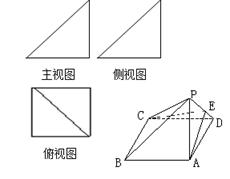
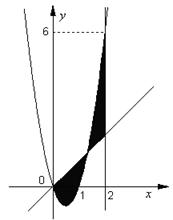
如图，已知二次函数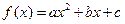
，直线
，直线
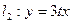（其中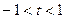
，
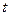为常数）；.若直线
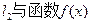的图象以及
的图象所围成的封闭图形如阴影所示.
（Ⅰ）求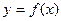
；
（Ⅱ）求阴影面积s关于t的函数
的解析式；
（Ⅲ）若过点
可作曲线
的三条切线，求实数m的取值范围.