有一种舞台灯,外形是正六棱柱ABCDEF—A1B1C1D1E1F1,在其每一个侧面上(不在棱上)安装5只颜色各异的彩灯,假若每只灯正常发光的概率是0.5,若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面. 假定更换一个面需100元,用ξ表示维修一次的费用.
(1)求面ABB1A1需要维修的概率;
(2)写出ξ的分布列,并求ξ的数学期望.
已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,椭圆上异于长轴顶点的任意点
,椭圆上异于长轴顶点的任意点 与左右两焦点
与左右两焦点 、
、 构成的三角形中面积的最大值为
构成的三角形中面积的最大值为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知点 ,连接
,连接 与椭圆的另一交点记为
与椭圆的另一交点记为 ,若
,若 与椭圆相切时
与椭圆相切时 、
、 不重合,连接
不重合,连接 与椭圆的另一交点记为
与椭圆的另一交点记为 ,求
,求 的取值范围.
的取值范围.
甲、乙两容器中分别盛有两种浓度的某种溶液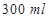 ,从甲容器中取出
,从甲容器中取出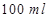 溶液,将其倒入乙容器中搅匀,再从乙容器中取出
溶液,将其倒入乙容器中搅匀,再从乙容器中取出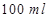 溶液,将其倒入甲容器中搅匀,这称为是一次调和,已知第一次调和后,甲、乙两种溶液的浓度分别记为:
溶液,将其倒入甲容器中搅匀,这称为是一次调和,已知第一次调和后,甲、乙两种溶液的浓度分别记为: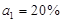 ,
, ,第
,第 次调和后的甲、乙两种溶液的浓度分别记为:
次调和后的甲、乙两种溶液的浓度分别记为: 、
、 .
.
(1)请用 、
、 分别表示
分别表示 和
和 ;
;
(2)问经过多少次调和后,甲乙两容器中溶液的浓度之差小于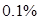 .
.
如图所示,空间中有一直角三角形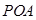 ,
, 为直角,
为直角,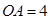 ,
,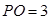 ,现以其中一直角边
,现以其中一直角边 为轴,按逆时针方向旋转
为轴,按逆时针方向旋转 后,将
后,将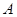 点所在的位置记为
点所在的位置记为 ,再按逆时针方向继续旋转
,再按逆时针方向继续旋转 后,
后,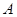 点所在的位置记为
点所在的位置记为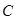 .
.
(1)连接 ,取
,取 的中点为
的中点为 ,求证:面
,求证:面 面
面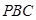 ;
;
(2)求 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.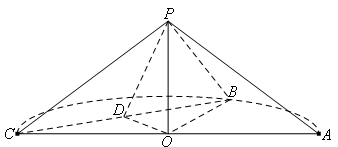
如图所示,某建筑工地准备建造一间两面靠墙的三角形露天仓库堆放材料,已知已有两面墙 、
、 的夹角为
的夹角为 (即
(即 ),现有可供建造第三面围墙的材料
),现有可供建造第三面围墙的材料 米(两面墙的长均大于
米(两面墙的长均大于 米),为了使得仓库的面积尽可能大,记
米),为了使得仓库的面积尽可能大,记 ,问当
,问当 为多少时,所建造的三角形露天仓库的面积最大,并求出最大值?
为多少时,所建造的三角形露天仓库的面积最大,并求出最大值? 
如图,一半径为 的圆形靶内有一个半径为
的圆形靶内有一个半径为 的同心圆,将大圆分成两
的同心圆,将大圆分成两
部分,小圆内部区域记为 环,圆环区域记为
环,圆环区域记为 环,某同学向该靶投掷
环,某同学向该靶投掷 枚飞镖,每次
枚飞镖,每次 枚. 假设他每次必
枚. 假设他每次必
定会中靶,且投中靶内各点是随机的.
(1)求该同学在一次投掷中获得 环的概率;
环的概率;
(2)设 表示该同学在
表示该同学在 次投掷中获得的环数,求
次投掷中获得的环数,求 的分布列及数学期望.
的分布列及数学期望.