如图,在三棱拄 中,
中, 侧面
侧面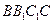 ,已知AA1=2,
,已知AA1=2, ,
,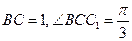
(Ⅰ)求证: ;
;
(Ⅱ)试在棱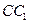 (不包含端点
(不包含端点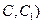 上确定一点
上确定一点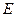 的位置,使得
的位置,使得 ;
;
(Ⅲ) 在(Ⅱ)的条件下,求二面角 的平面角的正切值.
的平面角的正切值.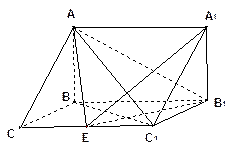
(本题满分12分)
已知集合 ,实数
,实数 使得集合
使得集合 满足
满足 ,
,
求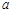 的取值范围.
的取值范围.
已知等差数列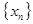 ,
,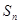 是
是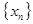 的前
的前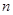 项和,且
项和,且 .
.
(1)求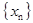 的通项公式;
的通项公式;
(2)设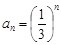 ,
, 是
是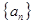 的前n项和,是否存在正数
的前n项和,是否存在正数 ,对任意正整数
,对任意正整数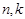 ,不等式
,不等式 恒成立?若存在,求
恒成立?若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(3)判断方程 是否有解,说明理由;
是否有解,说明理由;
动圆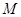 经过定点
经过定点 ,且与直线
,且与直线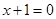 相切。
相切。
(1)求圆心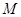 的轨迹
的轨迹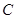 方程;
方程;
(2)直线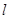 过定点
过定点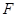 与曲线
与曲线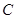 交于
交于 、
、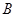 两点:
两点:
①若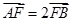 ,求直线
,求直线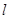 的方程;
的方程;
②若点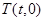 始终在以
始终在以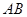 为直径的圆内,求
为直径的圆内,求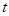 的取值范围。
的取值范围。
某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度h=4m,仰角∠ABE= ,∠ADE=
,∠ADE= 。
。
(1) 该小组已经测得一组 、
、 的值,tan
的值,tan =1.24,tan
=1.24,tan =1.20,请据此算出H的值;
=1.20,请据此算出H的值;
(2) 该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使 与
与 之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时,
之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时,

 最大?
最大?
如图,在直三棱柱 中,
中,
 ,
, ,
, 是
是 的中点.
的中点.
(1)求证: 平行平面
平行平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)试问线段 上是否存在点
上是否存在点 ,使
,使 与
与 成
成 角?若存在,确定
角?若存在,确定 点位置,若不存在,说明理由.
点位置,若不存在,说明理由.