已知平面直角坐标系中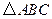 顶点的分别为
顶点的分别为 ,
,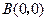 ,
,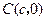 ,其中
,其中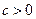 .
.
(1)若 ,求
,求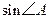 的值;(2)若
的值;(2)若 ,求
,求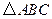 周长的最大值.
周长的最大值.
如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,点M在AD1上移动,点N在BD上移动,D1M=DN=a(0<a<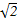 ),连接MN.
),连接MN.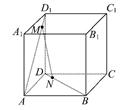
(1)证明对任意a∈(0,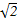 ),总有MN∥平面DCC1D1.
),总有MN∥平面DCC1D1.
(2)当a为何值时,MN的长最小?
如图所示,四边形EFGH所在平面为三棱锥A-BCD的一个截面,四边形EFGH为平行四边形.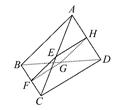
(1)求证:AB∥平面EFGH,CD∥平面EFGH.
(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.若M是线段AD的中点,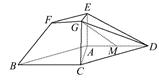
求证:GM∥平面ABFE.
如图,在正方体ABCD-A1B1C1D1中,E,F,G,M,N分别是B1C1,A1D1,A1B1,BD,B1C的中点,
求证:(1)MN∥平面CDD1C1.
(2)平面EBD∥平面FGA.
在四棱锥P -ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为60°.
(1)求四棱锥的体积.
(2)若E是PB的中点,求异面直线DE与PA所成角的余弦值.