(1)已知 ,
,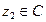 ,求证:
,求证: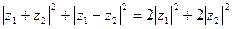
(2)已知 ,
,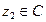 ,且
,且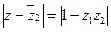 求证:
求证: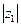 ,
,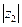 中至少有一个是1.
中至少有一个是1.
(本小题满分13分)已知椭圆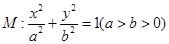 过点
过点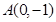 ,且离心率
,且离心率 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若椭圆 上存在点
上存在点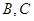 关于直线
关于直线 对称,求
对称,求 的所有取值构成的集合
的所有取值构成的集合 ,并证明对于
,并证明对于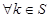 ,
, 的中点恒在一条定直线上.
的中点恒在一条定直线上.
(本小题满分14分)如图1,在梯形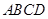 中,
中,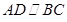 ,
,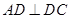 ,
,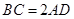 ,四边形
,四边形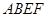 是矩形.将矩形
是矩形.将矩形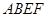 沿
沿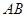 折起到四边形
折起到四边形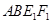 的位置,使平面
的位置,使平面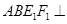 平面
平面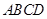 ,
,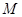 为
为 的中点,如图2.
的中点,如图2.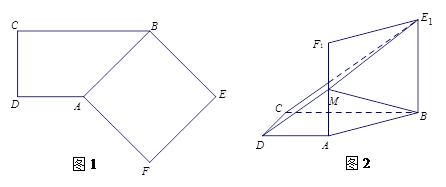
(Ⅰ)求证: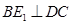 ;
;
(Ⅱ)求证: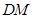 //平面
//平面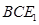 ;
;
(Ⅲ)判断直线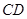 与
与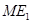 的位置关系,并说明理由.
的位置关系,并说明理由.
(本小题满分13分)在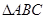 中,
中, .
.
(Ⅰ)若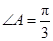 ,求
,求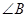 的大小;
的大小;
(Ⅱ)若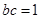 ,求
,求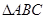 的面积的最大值.
的面积的最大值.
(本小题满分13分)某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,整理得到数据分组及频率分布表和频率分布直方图:
| 分组(日销售量) |
频率(甲种酸奶) |
| [ 0,10] |
0.10 |
| (10,20] |
0.20 |
| (20,30] |
0.30 |
| (30,40] |
0.25 |
| (40,50] |
0.15 |

(Ⅰ)写出频率分布直方图中的 的值,并作出甲种酸奶日销售量的频率分布直方图;
的值,并作出甲种酸奶日销售量的频率分布直方图;
(Ⅱ)记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为 ,
, ,试比较
,试比较 与
与 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计乙种酸奶在未来一个月(按30天计算)的销售总量.
(本小题满分13分)已知数列 的前
的前 项和为
项和为 ,
,  ,且
,且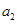 是
是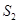 与
与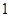 的等差中项.
的等差中项.
(Ⅰ)求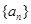 的通项公式;
的通项公式;
(Ⅱ)若数列 的前
的前 项和为
项和为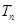 ,且对
,且对 ,
,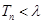 恒成立,求实数
恒成立,求实数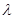 的最小值.
的最小值.