(本小题满分13分)已知椭圆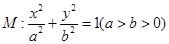 过点
过点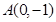 ,且离心率
,且离心率 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若椭圆 上存在点
上存在点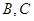 关于直线
关于直线 对称,求
对称,求 的所有取值构成的集合
的所有取值构成的集合 ,并证明对于
,并证明对于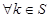 ,
, 的中点恒在一条定直线上.
的中点恒在一条定直线上.
(本小题满分10分). 选修4-5:不等式选讲
已知函数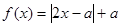 .
.
(1)若不等式 的解集为
的解集为 ,求实数
,求实数 的值;
的值;
(2)在(1)的条件下,若存在实数 使
使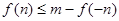 成立,求实数
成立,求实数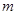 的取值范围.
的取值范围.
(本小题满分10分) 选修4-4:坐标系与参数方程
在直角坐标系 中, 过点
中, 过点 作倾斜角为
作倾斜角为 的直线
的直线 与曲线
与曲线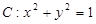 相交于不同的两点
相交于不同的两点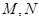 .
.
(1) 写出直线 的参数方程;
的参数方程;
(2) 求 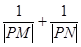 的取值范围.
的取值范围.
(本小题满分12分)
已知函数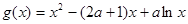
(1) 当 时, 求函数
时, 求函数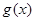 的单调增区间;
的单调增区间;
(2) 求函数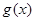 在区间
在区间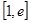 上的最小值;
上的最小值;
(3) 在(1)的条件下,设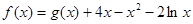 ,
,
证明: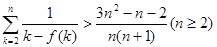 .参考数据:
.参考数据: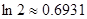 .
.
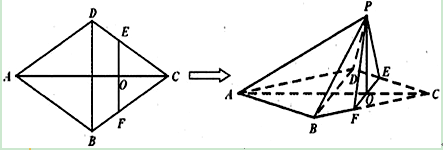
(本小题满分12分)
如图,在边长为4的菱形 中,
中,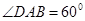 .点
.点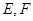 分别在边
分别在边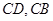 上,点
上,点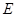 与点
与点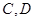 不重合,
不重合,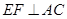 ,
,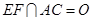 .沿
.沿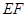 将
将 翻折到
翻折到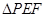 的位置,使平面
的位置,使平面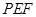 ⊥平面
⊥平面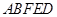 .
.
(1)求证: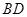 ⊥平面
⊥平面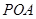 ;
;
(2)当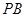 取得最小值时,请解答以下问题:
取得最小值时,请解答以下问题:
(i)求四棱锥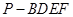 的体积;
的体积;
(ii)若点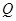 满足
满足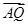 =
=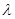
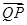 (
(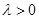 ),试探究:直线
),试探究:直线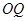 与平面
与平面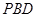 所成角的大小是否一定大于
所成角的大小是否一定大于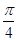 ?并说明理由.
?并说明理由.
(本小题满分12分)
假设某班级教室共有4扇窗户,在每天上午第三节课上课预备铃声响起时,每扇窗户或被敞开或被关闭,且概率均为0.5,记此时教室里敞开的窗户个数为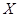 .
.
(1)求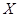 的分布列,以及
的分布列,以及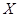 的数学期望;
的数学期望;
(2)若此时教室里有两扇或两扇以上的窗户被关闭,班长就会将关闭的窗户全部敞开,否则维持原状不变.记每天上午第三节课上课时该教室里敞开的窗户个数为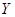 ,求
,求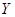 的数学期望.
的数学期望.