已知关于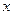 的方程
的方程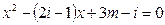 有实根,求实数
有实根,求实数 的取值。
的取值。
已知椭圆C: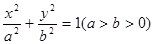 的左,右焦点分别为
的左,右焦点分别为 ,过
,过 的直线L与椭圆C相交 A,B于两点,且直线L的倾斜角为
的直线L与椭圆C相交 A,B于两点,且直线L的倾斜角为 ,点
,点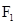 到直线L的距离为
到直线L的距离为 ,
,
(1)求椭圆C的焦距.(2)如果 求椭圆C的方程.(12分)
求椭圆C的方程.(12分)
如图,直三棱柱 中,
中,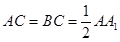 ,
,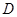 是棱
是棱 的中点,
的中点,
(1)证明: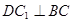
(2)求二面角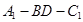 的大小. (12分)
的大小. (12分) 
已知棱长为a的正方体ABCD—A1B1C1D1,E为BC中点.
(1)求B到平面B1ED距离
(2)求直线DC和平面B1ED所成角的正弦值. (12分) 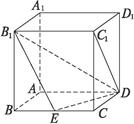
已知命题p: 方程 有两个大于-1的实数根,已知命题q:关于x的不等式
有两个大于-1的实数根,已知命题q:关于x的不等式 的解集是R,若“p或q”与“
的解集是R,若“p或q”与“ ” 同时为真命题,求实数a的取值范围(12分)
” 同时为真命题,求实数a的取值范围(12分)
已知双曲线的中心在原点,焦点 在坐标轴上,离心率为
在坐标轴上,离心率为 ,且过点(4,-
,且过点(4,-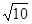 )(1)求双曲线的方程.(2)若点M(3,m)在双曲线上,求证:
)(1)求双曲线的方程.(2)若点M(3,m)在双曲线上,求证: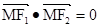 .(3)若点A,B在双曲线上,点N(3,1)恰好是AB的中点,求直线AB的方程(12分)
.(3)若点A,B在双曲线上,点N(3,1)恰好是AB的中点,求直线AB的方程(12分)