已知函数 在
在 处取得极值。
处取得极值。
(1)求 的极值。
的极值。
(2)当 时,求
时,求 的最大值。
的最大值。
已知函数 .
.
(Ⅰ)若点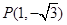 在角
在角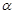 的终边上,求
的终边上,求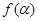 的值;
的值;
(Ⅱ)若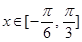 ,求
,求 的值域.
的值域.
(14分)已知定义在R上的函数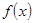 对任意
对任意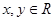 都有
都有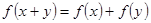 ,且当
,且当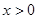 时,
时,
(1)求证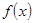 为奇函数;
为奇函数;
(2)判断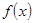 在R上的单调性,并用定义证明;
在R上的单调性,并用定义证明;
(3)若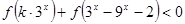 ,对任意
,对任意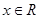 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
已知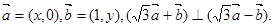
(1)求点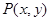 的轨迹C的方程;
的轨迹C的方程;
(2)若直线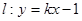 与曲线C交于A、B两点,并且A、B在y轴的同一侧,求实数k的取值范围.
与曲线C交于A、B两点,并且A、B在y轴的同一侧,求实数k的取值范围.
(3)设曲线C与x轴的交点为M,若直线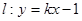 与曲线C交于A、B两点,是否存在实数k,使得以AB为直径的圆恰好过点M?若有,求出k的值;若没有,写出理由.
与曲线C交于A、B两点,是否存在实数k,使得以AB为直径的圆恰好过点M?若有,求出k的值;若没有,写出理由.
数列{an}满足
(1) 求数列{an}的通项公式;
(2) 若数列{bn}满足: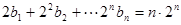 ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3) 令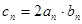 (n∈N*),求数列{cn}的前n项和Tn.
(n∈N*),求数列{cn}的前n项和Tn.
如图,已知四棱锥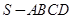 的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,
的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点, 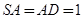 ,
,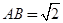 .
.
(1)求证:SA⊥平面ABCD
(2)求证:NF∥平面SAD;
(3)求二面角A-BN-C的余弦值.