已知函数 ,且 .
(I)试用含
的代数式表示
;
(Ⅱ)求
的单调区间;
(Ⅲ)令
,设函数
在
处取得极值,记点
,
,证明:线段
与曲线
存在异于
、
的公共点.
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
50 |
60 |
70 |
如果y与x之间具有线性相关关系.
(1)求这些数据的线性回归方程;
(2)预测当广告费支出为9百万元时的销售额.
由四个不同数字1,2,4,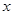 组成无重复数字的三位数,
组成无重复数字的三位数,
⑴若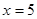 ,其中能被5整除的共有多少个?
,其中能被5整除的共有多少个?
⑵若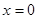 ,其中的偶数共有多少个?
,其中的偶数共有多少个?
⑶若所有这些三位数的各位数字之和是252,求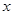 .
.
不等式选讲设函数 。
。
(Ⅰ)解不等式f(x)>2;
(Ⅱ)求函数y= f(x)的最小值。
在 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,已知
,已知 ,
, .
.
(Ⅰ)若 的面积等于
的面积等于 ,求
,求 ;
;
(Ⅱ)若 ,求
,求 的面积.
的面积.
已知正项数列{an},其前n项和Sn满足10Sn=an2+5an+6且a1,a3,a15成等比数列,求数列{an}的通项an