设向量 ,点
,点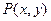 为动点,已知
为动点,已知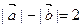 ,且点P的轨迹C1。若抛物线C2的顶点在原点,与轨迹C1共焦点F,设抛物线C2与轨迹C1的交点分别为M、N。
,且点P的轨迹C1。若抛物线C2的顶点在原点,与轨迹C1共焦点F,设抛物线C2与轨迹C1的交点分别为M、N。
(1)分虽求轨迹为C1与抛物线C2的方程;
(2)过F作一条与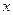 轴不垂直的直线,与曲线C1在点M、N左侧的部分交于C、D两点,与曲线C2在点M、N左侧的部分交于B、E两点,若G为CD的中点,H为BE的中点,问
轴不垂直的直线,与曲线C1在点M、N左侧的部分交于C、D两点,与曲线C2在点M、N左侧的部分交于B、E两点,若G为CD的中点,H为BE的中点,问 是否为定值?若是,求出定值;若不是,请说明理由。
是否为定值?若是,求出定值;若不是,请说明理由。
(本小题满分14分)一个口袋中装有 个红球
个红球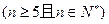 和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
(1)试用 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率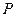 ;
;
(2)若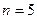 ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
(3)记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为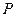 ,当
,当 取多少时,
取多少时,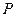 最大?
最大?
(本小题满分12分)现有分别写有数字1,2,3,4,5的5张白色卡片、5张黄色卡片、5张红色卡片。每次试验抽一张卡片,并定义随机变量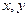 如下:若是白色,则
如下:若是白色,则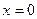 ;若是黄色,则
;若是黄色,则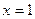 ;若是红色,则
;若是红色,则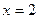 ;若卡片数字是
;若卡片数字是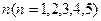 ,则
,则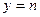
(1)求概率
(2)求数字期望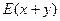 与数字方差
与数字方差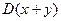
(本小题满分12分)上海世博会举办时间为2010年5月1日~10月31日。福建馆以“海西”为参博核心元素,主题为“潮涌海西,魅力福建”。福建馆招募了60名志愿者,某高校有l3人入选,其中5人为中英文讲解员,8人为迎宾礼仪,它们来自该校的5所所学院(这5所学院编号为1~5号),人员分布如图所示。若从这13名入选者中随机抽取3人。
(1)求这3人所在学院的编号恰好成等比数列的概率;
(2)求这3人中中英文讲解员人数的分布列及数学期望。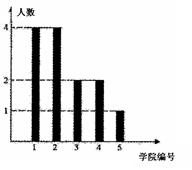
(本小题满分12分)带有编号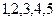 的五个球
的五个球
(1)全部投入4个不同的盒子里,有多少种不同的方法?
(2)放进4个不同的盒子里,每盒一个,有多少种不同的方法?
(3)将其中的4个球投入4个盒子里的一个(另一球不投入),有多少种不同的方法?
(4)全部投入4个不同的盒子里,没有空盒,有多少种不同的放法?
(本小题满分12分)已知二阶矩阵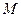 有特征值
有特征值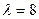 及对应的一个特征向量
及对应的一个特征向量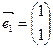 ,并且矩阵
,并且矩阵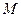 对应的变换将点(-1,2)变换成(-2,4).
对应的变换将点(-1,2)变换成(-2,4).
(1)求矩阵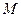
(2)求矩阵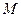 的另一个特征值及对应的一个特征向量
的另一个特征值及对应的一个特征向量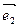 的坐标之间关系
的坐标之间关系
(3)求直线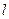 :
: 在矩阵
在矩阵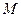 的作用下的直线
的作用下的直线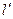 的方程
的方程