在△ABC中,角A、B、C所对的边分别是a,b,c,且
(1)求 的值;
的值;
(2)若b=2,求△ABC面积的最大值.
(本小题满分14分 )
)
若由数列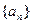 生成的数列
生成的数列 满足对任意的
满足对任意的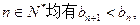 其中
其中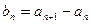 ,则称数列
,则称数列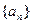 为“Z数列”。
为“Z数列”。
(I)在数列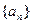 中,已知
中,已知 ,试判断数列
,试判断数列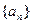 是否为“Z数列”;
是否为“Z数列”;
( II)若数列
II)若数列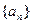 是“Z数列”,
是“Z数列”,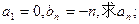
(III)若数列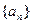 是“Z数列”,设
是“Z数列”,设 求证
求证
(本小题满分14分)
设函数
(I)求函数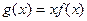 在区间[0,1]上的最小值;
在区间[0,1]上的最小值;
(II)当 时,记曲线
时,记曲线 在点
在点 处的切线为
处的切线为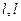 与x轴交于点
与x轴交于点 ,求证:
,求证:
(本小题满分14分)
已知椭圆 的离心率为
的离心率为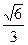 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6。
,椭圆C上任意一点到椭圆两个焦点的距离之和为6。
(I)求椭圆C的方程;
(II)设直线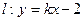 与椭圆C交于A、B两点,点P(0,1),且|PA|=|PB|,求直线
与椭圆C交于A、B两点,点P(0,1),且|PA|=|PB|,求直线 的方程。
的方程。
(本小题满分13分) 如图,已知四棱柱ABCD—A1B1C1D1的底面是菱形,侧棱BB1⊥底面ABCD,E是侧棱CC1的中点。
如图,已知四棱柱ABCD—A1B1C1D1的底面是菱形,侧棱BB1⊥底面ABCD,E是侧棱CC1的中点。
(I)求证:AC⊥平面BDD1B1;
(II)求证:AC//平面B1DE。
(本小题满分15分)
在参加市里主办的科技知识竞赛的学生中随机选取了40名学生的成绩作为样本,这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式 分成6组:第一组,成绩大于等于40分且小于50分;第二组,成绩大于等于50分且小于60分;……第六组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图。
分成6组:第一组,成绩大于等于40分且小于50分;第二组,成绩大于等于50分且小于60分;……第六组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图。
在选取的40名学生中。
(I)求成绩在区间 内的学生人数;
内的学生人数;
(II)从成绩大于等于80分的学生中随机选2名学生,求至少有1名学生成绩在区间[90,100]内的概率。