设 ,
, , 其中
, 其中 是不等于零的常数,
是不等于零的常数,
(1)、(理)写出 的定义域;
的定义域;
(文) 时,直接写出
时,直接写出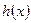 的值域
的值域
(2)、(文、理)求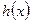 的单调递增区间(理5分,文8分);
的单调递增区间(理5分,文8分);
(3)、已知函数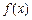
 ,定义:
,定义: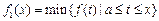
 ,
,
 .其中,
.其中, 表示函数
表示函数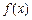 在
在 上的最小值,
上的最小值,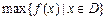 表示函数
表示函数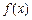 在
在
 上的最大值.例如:
上的最大值.例如: ,
, ,则
,则 ,
, ,
,
(理)当 时,设
时,设 ,不等式
,不等式
恒成立,求 的取值范围;
的取值范围;
(文)当 时,
时, 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(文科做以下(1)(2)(3))
(1)、已知 ,求数列
,求数列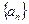 的通项公式;
的通项公式;
(2)、在(1)的条件下,数列 ,求证数列
,求证数列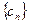 是一个 “1类和科比数列”;
是一个 “1类和科比数列”;
(3)、设等差数列 是一个 “
是一个 “ 类和科比数列”,其中首项
类和科比数列”,其中首项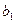 ,公差
,公差 ,探究
,探究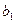
与 的数量关系,并写出相应的常数
的数量关系,并写出相应的常数 ;
;
数列 的前n项和记为
的前n项和记为 ,前
,前 项和记为
项和记为
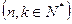 ,对给定的常数
,对给定的常数 ,若
,若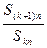 是与
是与 无关的非零常数
无关的非零常数 ,则称该数列
,则称该数列 是“
是“ 类和科比数列”,
类和科比数列”,
(理科做以下(1)(2)(3))
(1)、已知 ,求数列
,求数列 的通项公式;
的通项公式;
(2)、证明(1)的数列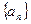 是一个 “
是一个 “ 类和科比数列”;
类和科比数列”;
(3)、设正数列 是一个等比数列,首项
是一个等比数列,首项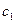 ,公比
,公比
 ,若数列
,若数列 是一个 “
是一个 “ 类和科比数列”,探究
类和科比数列”,探究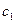 与
与 的关系
的关系
(文)已知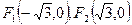 ,点
,点 满足
满足 ,记点
,记点 的轨迹为E,
的轨迹为E,
(1)、求轨迹E的方程;
(2)、如果过点Q(0,m)且方向向量为 ="(1,1)" 的直线l与点P的轨迹交于A,B两点,当
="(1,1)" 的直线l与点P的轨迹交于A,B两点,当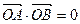 时,求
时,求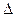 AOB的面积。
AOB的面积。
(理)已知 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设
 =
= ,
, 
 =,且满足
=,且满足
(1)、求点P(x,y)的轨迹E的方程.
(2)、若直线 过点
过点
 且法向量为
且法向量为 ,直线与轨迹
,直线与轨迹 交于
交于 两点.点
两点.点 ,无论直线
,无论直线 绕点
绕点 怎样转动,
怎样转动,  是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数
是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数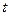 的取值范围;
的取值范围;