已知函数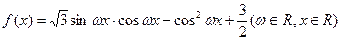 的最小正周期为
的最小正周期为 ,且当
,且当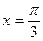 时,函数取最大值.
时,函数取最大值.
(1)求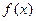 的解析式;
的解析式;
(2)试列表描点作出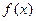 在[0,
在[0, ]范围内的图象.
]范围内的图象.
已知函数
(Ⅰ)若关于 的不等式
的不等式 的解集为
的解集为 ,求实数
,求实数 的值;
的值;
(Ⅱ)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
已知函数
(Ⅰ)当 时,解不等式
时,解不等式 ;
;
(Ⅱ)若 的最小值为1,求
的最小值为1,求 的值
的值
已知椭圆C的方程为 ,如图所示,在平面直角坐标系
,如图所示,在平面直角坐标系 中,
中, 的三个顶点的坐标分别为
的三个顶点的坐标分别为
(Ⅰ)当椭圆C与直线 相切时,求
相切时,求 的值;
的值;
(Ⅱ)若椭圆C与 三边无公共点,求
三边无公共点,求 的取值范围;
的取值范围;
(Ⅲ)若椭圆C与 三边相交于不同的两点M,N,求
三边相交于不同的两点M,N,求 的面积
的面积 的最大值.
的最大值.
设函数 是自然对数的底数)
是自然对数的底数)
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若关于 的方程
的方程 在区间
在区间 上恰有两相异实根,求
上恰有两相异实根,求 的取值范围;
的取值范围;
(Ⅲ)当 时,证明:
时,证明:
新建的荆州中学拟模仿图甲建造一座体育馆,其设计方案侧面的外轮廓线如图乙所示:曲线 是以点
是以点 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中 单位:米
单位:米 ;曲线
;曲线 是抛物线
是抛物线 的一部分;
的一部分; ,且
,且 恰好等于圆
恰好等于圆 的半径.假定拟建体育馆的高
的半径.假定拟建体育馆的高 米.
米.
(Ⅰ)若要求 米,
米,  米,求
米,求 与
与 的值;
的值;
(Ⅱ)若 ,将
,将 的长表示为点
的长表示为点 的纵坐标
的纵坐标 的函数
的函数 ,并求
,并求 的最大值.
的最大值.
并求 的最大值.(参考公式:若
的最大值.(参考公式:若 ,则
,则 ,其中
,其中 为常数)
为常数)