袋中装有大小相同的2个白球和3个黑球.
(Ⅰ)采取放回抽样方式,从中依次摸出两个球,求两球颜色不同的概率;
(Ⅱ)采取不放回抽样方式,从中依次摸出两个球,记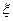 为摸出两球中白球的个数,求
为摸出两球中白球的个数,求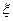 的期望和方差.
的期望和方差.
如图,平行四边形 中, 将 沿 折起到 的位置,使平面 平面 .
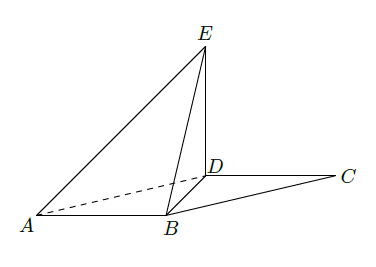
(Ⅰ)求证:
;
(Ⅱ)求三棱锥
的侧面积.
对于数列
,若存在常数
,对任意的
,恒有
,则称数列
为
数列.
(Ⅰ)首项为1,公比为
的等比数列是否为
数列?请说明理由;
(Ⅱ)设
是数列
的前
项和,给出下列两组判断:
A组:①数列
是
数列;②数列
不是
数列;
B组:③数列
是
数列;④数列
不是
数列.
请以其中一组中的一个论断为条件,另一组中的一个论断为结论组成一个命题。判断所给命题的真假,并证明你的结论;
(Ⅲ)若数列
是
数列,证明:数列
也是
数列.
已知函数
的导函数的图象关于直线
对称.
(Ⅰ)求
的值;
(Ⅱ)若
在
处取得最小值,记此极小值为
,求
的定义域和值域.
如图,在正三棱柱 中, , ,点 是 的中点,点 在 上,且 .
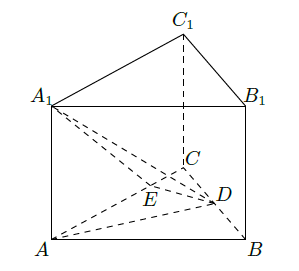
(Ⅰ)证明:平面
(Ⅱ)求直线AD和平面 所成角的正弦值。
已知函数
(其中
)的周期为
,且图象上一个最低点为
.
(Ⅰ)求
的解析式;
(Ⅱ)当
,求
的最值.