已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性即没患病.下面是两种化验方案:
方案甲:逐个化验,直到能确定患病动物为止;
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验。
求依方案甲所需化验次数不少于依方案乙所需化验次数的概率。
(本小题满分12分)“一站到底”是某电视台推出的大型游戏益智节目.为了统计某市观众节目播出当日收视情况,随机抽查了该市 名市民的收视情况,得到如下数据统计表(如图(1)):
名市民的收视情况,得到如下数据统计表(如图(1)):
若收看时间超过 小时的观众定义为“智趣观众”,收看时间不超过
小时的观众定义为“智趣观众”,收看时间不超过 小时的观众定
小时的观众定
义为“非智趣观众”,已知“非智趣观众”与“智趣观众”人数比恰好为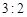 .
.
(1)试确定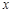 ,
,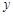 ,
,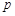 ,
,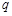 的值,并补全频率分布直方图(如图 (2)).
的值,并补全频率分布直方图(如图 (2)).
(2)节目组为了进一步了解这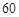 名观众的收视观感,从“非智趣观众”与“智趣观众”中用分层抽样的方法确定
名观众的收视观感,从“非智趣观众”与“智趣观众”中用分层抽样的方法确定 人,若需从这
人,若需从这 人中随机选取
人中随机选取 人进行问卷调查.设
人进行问卷调查.设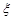 为选取的
为选取的 人中“智趣观众”的人数,求
人中“智趣观众”的人数,求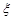 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)如图所示,直线
 平面
平面 ,且四边形
,且四边形 为矩形,四边形
为矩形,四边形 为直角梯形,
为直角梯形, ,
,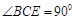 ,
,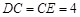 ,
, .
.
(1)求证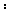
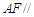 平面
平面 ;
;
(2)求平面 与平面
与平面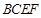 所成锐二面角的余弦值.
所成锐二面角的余弦值.
已知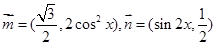 ,
,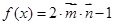 .
.
(Ⅰ)求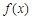 的最大值及取得最大值时
的最大值及取得最大值时 的值;
的值;
(Ⅱ)在 中,角
中,角 ,
,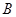 ,
,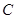 的对边分别为
的对边分别为 若
若 ,
, ,
,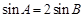 ,求
,求 的面积.
的面积.
设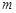 是给定的正整数,有序数组(
是给定的正整数,有序数组( )中
)中 或
或
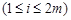 .
.
(1)求满足“对任意的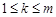 ,
, ,都有
,都有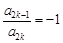 ”的有序数组(
”的有序数组( )的个数
)的个数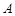 ;
;
(2)若对任意的 ,
,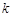 ,
, ,都有
,都有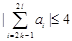 成立,求满足“存在
成立,求满足“存在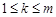 ,使得
,使得 ”的有序数组(
”的有序数组( )的个数
)的个数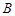 .
.
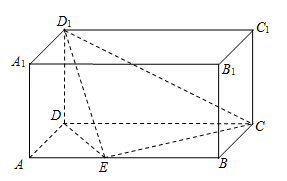
在长方体ABCD—A1B1C1D1中, ,点E是棱AB上一点.且
,点E是棱AB上一点.且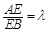 .
.
(1)证明: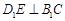 ;
;
(2)若二面角D1—EC—B的大小为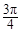 ,求
,求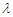 的值.
的值.