已知椭圆C: +
+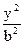 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。
,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。
(1)求直线ON(O为坐标原点)的斜率KON ;
(2)对于椭圆C上任意一点M,试证:总存在角 (
( ∈R)使等式:
∈R)使等式: =cos
=cos
 +sin
+sin
 成立。
成立。
((本小题满分14分)
已知圆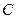 的圆心为
的圆心为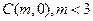 ,半径为
,半径为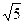 ,圆
,圆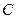 与椭圆
与椭圆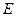 :
: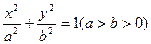 有一个公共点
有一个公共点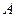 (3,1),
(3,1),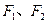 分别是椭圆的左、右焦点.
分别是椭圆的左、右焦点.
(1)求圆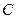 的标准方程;
的标准方程;
(2)若点P的坐标为(4,4),试探究斜率为k的直线
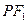 与圆
与圆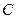 能否相切,若能,求出椭圆
能否相切,若能,求出椭圆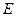 和直线
和直线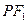 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
(本小题满分14分)
图为一简单组合体,其底面ABCD为正方形, 平面
平面 ,
, ,
,
且 ,
,
(1)求证: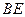 //平面
//平面 ;
;
(2)若N为线段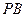 的中点,求证:
的中点,求证: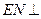 平面
平面 ;
;
(本小题满分12分)某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
| 积极参加班级工作 |
不太主动参加班级工作 |
 合计 合计 |
|
| 学习积极性高 |
18 |
7 |
25 |
| 学习积极性一般 |
6 |
19 |
25 |
| 合计 |
24 |
26 |
50 |
(1)如果随机调查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是 多少?抽到不太积极参加班级工作且学习积极性一般的学生的概率是多少?
多少?抽到不太积极参加班级工作且学习积极性一般的学生的概率是多少?
(2)学生的积极性与对待班级工作的态度是否有关系?说明理由.
函数
的部分图象如图所示
(1)求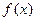 的最小正周期及解析式;
的最小正周期及解析式;
(2)设 求函数
求函数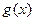 在区间
在区间 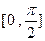 上的最大值和最小值.
上的最大值和最小值.
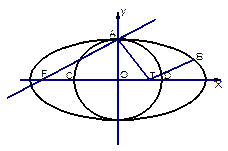
已知圆o: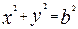 与椭圆
与椭圆 有一个公共点A(0,1),F为椭圆的左焦点,直线AF被圆所截得的弦长为1.
有一个公共点A(0,1),F为椭圆的左焦点,直线AF被圆所截得的弦长为1.
(1)求椭圆方程。
(2)圆o与x轴的两个交点为C、D,B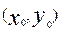 是椭圆上异于点A的一个动点,在线段CD上是否存在点T
是椭圆上异于点A的一个动点,在线段CD上是否存在点T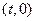 ,使
,使 ,若存在,请说明理由。
,若存在,请说明理由。