设函数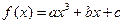
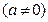 为奇函数,其图象在点
为奇函数,其图象在点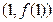 处的切线与直线
处的切线与直线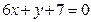 平行,导函数
平行,导函数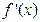 的最小值为
的最小值为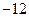

(Ⅰ)求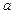 ,
,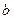 ,
,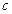 的值;
的值;
(Ⅱ)求函数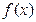 的单调递增区间,并求函数
的单调递增区间,并求函数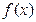 在
在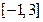 上的最大值和最小值
上的最大值和最小值
(本小题满分13分)如图所示的茎叶图记录了甲、乙两组各四名同学的投篮命中次数, 乙组记录中有一个数据模糊,无法确认, 在图中以 表示.
表示.
(Ⅰ)如果乙组同学投篮命中次数的平均数为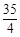 , 求
, 求 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;
(Ⅱ)在(Ⅰ)的条件下, 分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名, 记事件A:“两名同学的投篮命中次数之和为17”, 求事件A发生的概率.
(本小题满分12分)下图是调查某地某公司1000名员工的月收入后制作的直方图.根据直方图估计:
(Ⅰ)该公司月收入在1000元到1500元之间的人数;
(Ⅱ)该公司员工的月平均收入;
(Ⅲ)该公司员工收入的众数;
(Ⅳ)该公司员工月收入的中位数;
已知椭圆 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=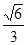 ,过点A(0,-b)和B(a,0)的直线与坐标原点距离为
,过点A(0,-b)和B(a,0)的直线与坐标原点距离为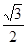 .
.
(1)求椭圆的方程;
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆相交于C、D两点,试判断是否存在k值,使以CD为直径的圆过定点E?若存在求出这个k值,若不存在说明理由.
若点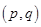 ,在
,在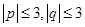 中按均匀分布出现.
中按均匀分布出现.
(1)点 横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点
横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点 落在上述区域的概率?
落在上述区域的概率?
(2)试求方程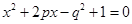 有两个实数根的概率.
有两个实数根的概率.
已知方程 ,设
,设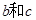 分别是先后抛掷一枚骰子得到的点数. 求方程
分别是先后抛掷一枚骰子得到的点数. 求方程 有实根的概率;
有实根的概率;