已知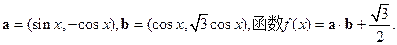
（1）求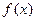
的最小正周期，并求其图象对称中心的坐标；
（2）当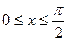
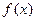时，求函数的值域。
（本小题满分12分）
双曲线
，一焦点到其相应准线的距离为
，过点A（0，-b），B（a，0）的直线与原点的距离为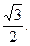
（1）求该双曲线的方程
（2）是否存在直线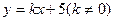
与双曲线交于相异两点C，D，使得C，D两点都在以A为圆心的同一个圆上，若存在，求出直线方程；若不存在说明理由.
本小题满分12分）
|
已知斜三棱柱ABC—A1B1C1，
在底面ABC上的射影恰为AC的中点D，又知
设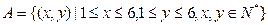
（1）求从A中任取一个元素是（1，2）的概率；
（2）从A中任取一个元素，求
的概率
（理）（3）设
为随机变量，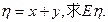
（2）设从A中任取一个元素，的事件为C，有
（4，6）（6，4）（5，5）（5，6）（6，5）（6，6）
（本小题满分10分）
已知不等式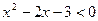
的解集为A，不等式
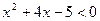的解集为B，
（1）求
（2）若不等式
的解集是，求
的解集.
（本小题满分12分）
某食品厂定期购买面粉，已知该厂每天需要面粉6吨，每吨面粉的价格为1800元，面粉的保管等其它费用为平均每吨每天3元，购面粉每次需支付运费900元.求该厂多少天购买一次面粉，才能使平均每天所支付的总费用最少？
