设数列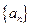
的前
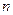项的和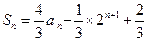
，
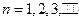
（Ⅰ）求首项
与通项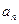
；
（Ⅱ）设
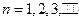，，证明：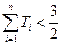
.
有一批食品出厂前要进行五项指标检验，如果有两项指标不合格，则这批食品不能出厂．已知每项指标抽检是相互独立的，且每项抽检出现不合格的概率都是
．
（1）求这批产品不能出厂的概率(保留三位有效数字)；
(2)求直至五项指标全部验完毕，才能确定该批食品是否出厂的概率(保留三位有效数字)．
某保险公司新开设了一项保险业务，若在一年内事件
发生，该公司要赔偿
元．设在一年内发生的概率为
，为使公司收益的期望值等于的百分之十，公司应要求顾客交多少保险金？
甲乙两人独立解某一道数学题，已知该题被甲独立解出的概率为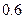
，被甲或乙解出的概率为
，（1）求该题被乙独立解出的概率；（2）求解出该题的人数
的数学期望和方差
要制造一种机器零件，甲机床废品率为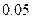
，而乙机床废品率为
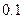，而它们
的生产是独立的，从它们制造的产品中，分别任意抽取一件，求：
（1）其中至少有一件废品的概率；（2）其中至多有一件废品的概率.
三个元件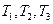
正常工作的概率分别为
将它们中某两个元件并联后再和第三元件串联接入电路.
（Ⅰ）在如图的电路中，电路不发生故障的概率是多少？
|
（Ⅱ）三个元件连成怎样的电路，才能使电路中不发生故障的概率最大？请画出此时电路图，并说明理由.
