已知为实常数），且，其图象和y轴交于A点；数列为公差为的等差-优题课

已知为实常数），且，其图象和y轴交于A点；数列为公差为的等差数列，且；点列
（1）求函数的表达式；
（2）设为直线的斜率，的斜率，求证数仍为等差数列；
（3）已知m为一给定自然数，常数a满足，求证数列有唯一的最大项.

科目数学题型解答题难度较易

为了了解一个小水库中养殖的鱼有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量（单位：千克），并将所得数据分组，画出频率分布直方图（如图所示）

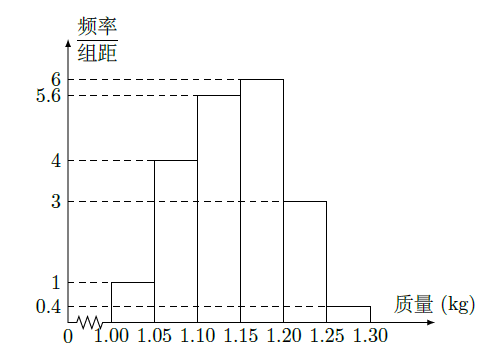
（Ⅰ）在答题卡上的表格中填写相应的频率；
（Ⅱ）估计数据落在（1.15,1.30）中的概率为多少；
（Ⅲ）将上面捕捞的100条鱼分别作一记号后再放回水库，几天后再从水库的多处不同位置捕捞出120条鱼，其中带有记号的鱼有6条，请根据这一情况来估计该水库中鱼的总条数。

已经函数 $f (x) = \frac{\cos^{2} x - \sin^{2} x}{2}, g (x) = \frac{1}{2} \sin 2 x - \frac{1}{4}$

(Ⅰ)函数 $f (x)$ 的图象可由函数 $g (x)$ 的图象经过怎样变化得出？
(Ⅱ)求函数 $h (x) = f (x) - g (x)$ 的最小值，并求使用 $h (x)$ 取得最小值的 $x$ 的集合。

已知函数 $f (x) = a x + \frac{b}{x} + c (a > 0)$ 的图象在点 $(1, f (1))$ 处的切线方程为 $y = x - 1$ .

(I)用 $a$ 表示出 $b, c$ ;

(II)若 $f (x) \geq \ln x$ 在 $[1, + \infty)$ 上恒成立，求 $a$ 的取值范围；

(III)证明： $1 + \frac{1}{2} + \frac{1}{3} + . . . + \frac{1}{n} > \ln (n + 1) + \frac{n}{2 (n + 1)} (n \geq 1)$ .

已知数列 ${a_{n}}$ 满足： $a_{1} = \frac{1}{2}$ ， $\frac{3 (1 + a_{n + 1})}{1 - a_{n}} = \frac{2 (1 + a_{n})}{1 - a_{n + 1}}$ , $a_{n} a_{n + 1} ＜ 0 （ n \geq 1 ）$ ；数列_{${b_{n}}$}满足： $b_{n} = {a_{n + 1}}^{2} - {a_{n}}^{2} （ n \geq 1 ）$ .

（1）求数列 ${a_{n}}$ ， ${b_{n}}$ 的通项公式；

（2）证明：数列 ${b_{n}}$ 中的任意三项不可能成等差数列。

如图，在四面体 $A B O C$ 中, $O C ⊥ O A, O C ⊥ O B, ∠ A O B = 120^{°}$ , 且 $O A = O B = O C = 1$ .

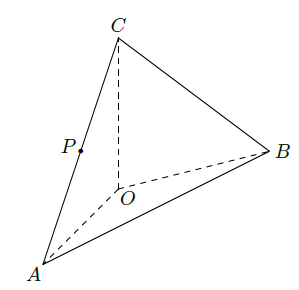
（Ⅰ）设为 $P$ 为 $A C$ 的中点，证明：在 $A B$ 上存在一点 $Q$ ，使 $P Q ⊥ O A$ ，并计算 $\frac{A B}{A Q}$ 的值；
（Ⅱ）求二面角 $O - A C - B$ 的平面角的余弦值.

试卷网试题网古诗词网作文网范文网