(本小题满分12分)
袋内装有6个球,每个球上都记有从1到6的一个号码,设号码为n的球重 克,这些球等可能地从袋里取出(不受重量、号码的影响)。
克,这些球等可能地从袋里取出(不受重量、号码的影响)。
(1)如果任意取出1球,求其重量大于号码数的概率;
(2)如果不放回地任意取出2球,求它们重量相等的概率。
甲乙两人连续6年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图: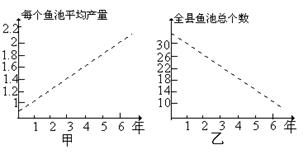
甲调查表明:每个鱼池平均产量从第1年1万只鳗鱼上升到第6年2万只。
乙调查表明:全县鱼池总个数由第1年30个减少到第6年10个。
请你根据提供的信息说明:
(Ⅰ)第2年全县鱼池的个数及全县出产的鳗鱼总数。
(Ⅱ)到第6年这个县的鳗鱼养殖业的规模(即总产量)比第1年扩大了还是缩小了?说明理由。
(Ⅲ)哪一年的规模(即总产量)最大?说明理由。
已知数列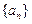 满足:
满足: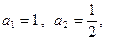 且
且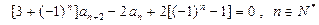 .
.
(Ⅰ)求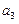 ,
, ,
,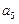 ,
,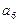 的值及数列
的值及数列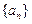 的通项公式;
的通项公式;
(Ⅱ)设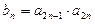 ,求数列
,求数列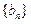 的前
的前 项和
项和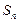 ;
;
在四棱锥 中,
中,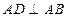 ,
,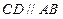 ,
,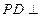 底面
底面 ,
,  ,直线
,直线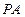 与底面
与底面 成
成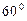 角,点
角,点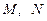 分别是
分别是 的中点.
的中点.
(1)求二面角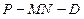 的大小;
的大小;
(2)当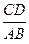 的值为多少时,
的值为多少时,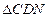 为直角三角形.
为直角三角形.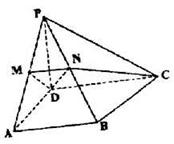
如图,已知正方体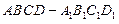 的棱长为2,E、F分别是
的棱长为2,E、F分别是 、
、 的中点,过
的中点,过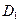 、E、F作平面
、E、F作平面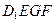 交
交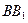 于G..
于G..
(Ⅰ)求证: ∥
∥ ;
;
(Ⅱ)求二面角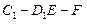 的余弦值;
的余弦值;
(Ⅲ)求正方体被平面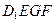 所截得的几何体
所截得的几何体 的体积.
的体积.
已知数列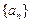 满足:
满足: 且
且 .
.
(Ⅰ)求 ,
, ,
, ,
, 的值及数列
的值及数列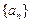 的通项公式;
的通项公式;
(Ⅱ)设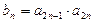 ,求数列
,求数列 的前
的前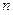 项和
项和 ;
;