(本小题满分12分) 已知函数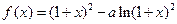
在
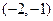上是增函数，在
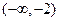上为减函数.
(Ⅰ)求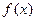
的表达式；
(Ⅱ)若当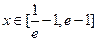
时，不等式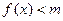
恒成立，求实数
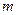的值；
（Ⅲ）是否存在实数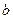
使得关于
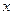的方程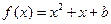
在区间［0，2］上恰好有两个相异的实根，若存在，求实数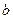的取值范围.
在四棱锥P—ABCD中，底面ABCD是a的正方形，PA⊥平面ABCD，
且PA=2AB
（1）求证：平面PAC⊥平面PBD；
（2）求二面角B—PC—D的余弦值.
（．如图所示，已知四棱锥P—ABCD，底面ABCD为菱形，PA⊥平面ABCD，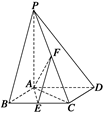
∠ABC=60°,E,F分别是BC,PC的中点.
(1)证明:AE⊥PD;
(2)若H为PD上的动点,EH与平面PAD所成最大角的正切值为
,
求二面角E—AF—C的余弦值.
（如图所示，在四棱锥P—ABCD中，底面为直角梯形，AD∥BC，∠BAD=90°，PA⊥底面ABCD，且PA=AD=AB=2BC，M、N分别为PC、PB的中点.
（1）求证：PB⊥DM；
（2）求BD与平面ADMN所成的角.
（在正四面体P—ABC中,D,E,F分别是AB、BC、 CA的中点,求证: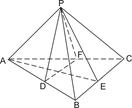
（１）BC∥平面PDF;（２）BC⊥平面PAE
(本题12分) 设函数
．
(1) 求函数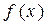
的单调区间；
(2) 若函数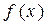在区间(0,2)上单调递减，试求实数
的取值范围；
(3) 若函数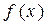的极小值大于0，试求实数的取值范围．