为了了解高一女生的身高情况,某中学对高一某班女生的身高(单位: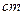 )进行了一次测量,所得数据整理后列出了频率分布表如下:
)进行了一次测量,所得数据整理后列出了频率分布表如下:
| 组 别 |
频数 |
频率 |
| [145.5,149.5) |
1 |
0.02 |
| [149.5,153.5) |
4 |
0.08 |
| [153.5,157.5) |
20 |
0.40 |
| [157.5,161.5) |
15 |
0.30 |
| [161.5,165.5) |
8 |
0.16 |
| [165.5,169.5] |
 |
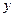 |
| 合 计 |
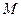 |
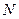 |
(Ⅰ)求出表中 、
、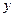 、
、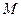 、
、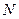 所表示的数值;
所表示的数值;
(Ⅱ)画出频率分布直方图;
(Ⅲ)估计高一女生身高在[155,165]的概率.
如图,四棱锥P-ABCD的底面是平行四边形,PA⊥平面ABCD, ,
,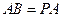 ,点E是PD上的点,且DE=
,点E是PD上的点,且DE= PE(0<
PE(0<
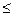 1).
1).
(Ⅰ) 求证:PB⊥AC;
(Ⅱ) 求 的值,使
的值,使 平面ACE;
平面ACE;
(Ⅲ) 当 时,求二面角E-AC-B的大小.
时,求二面角E-AC-B的大小.
设函数f(x)=2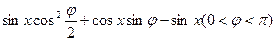 在
在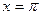 处取最小值.(Ⅰ) 求
处取最小值.(Ⅰ) 求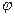 的值;(Ⅱ)在
的值;(Ⅱ)在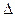 ABC中,
ABC中,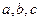 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知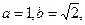
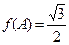 ,求角C.
,求角C.
小李、小王、小张三人在一起做游戏时,需要确定做游戏的先后顺序,他们约定用“剪刀、布、锤子”的方式确定,在一个回合中.求:
(Ⅰ) 恰有一人出“布”的概率;
(Ⅱ) 至少有一人出“布”的概率.
已知函数 ,满足:①对任意
,满足:①对任意 ,都有
,都有
 ;
;
②对任意n∈N *都有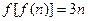 .
.
(Ⅰ)试证明: 为
为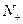 上的单调增函数;
上的单调增函数;
(Ⅱ)求 ;
;
(Ⅲ)令 ,试证明:
,试证明:
函数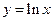 关于直线
关于直线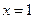 对称的函数为
对称的函数为 ,又函数
,又函数 的导函数为
的导函数为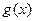 ,记
,记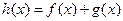 .
.
(Ⅰ)设曲线 在点
在点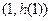 处的切线为
处的切线为 ,
,  与圆
与圆 相切,求
相切,求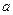 的值;
的值;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)求函数 在[0,1]上的最大值.
在[0,1]上的最大值.